Распределение Фишера-Снедекора

Плотность распределения случайной величины Фишера-Снедекора или F-распределения определяется по формуле:

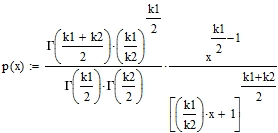
k₁ и k₂ — степени свободы;

Γ(y) — гамма-функция Эйлера.

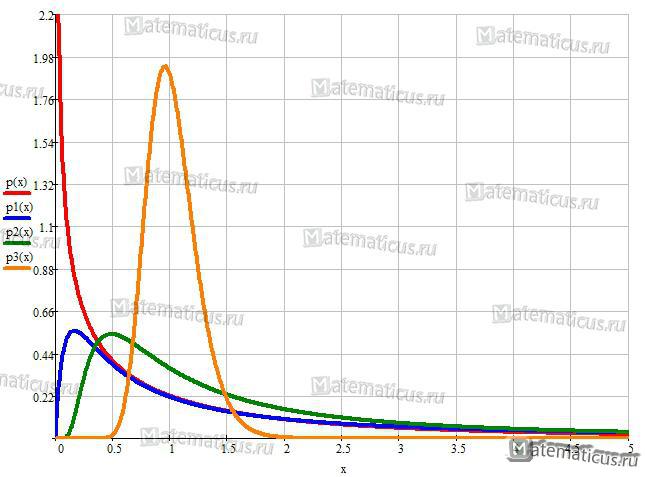
График плотности вероятности при k₁=1 и k₂=5, k₁=1 и k₂=4, k₁=90 и k₂=2, k₁=90 и k₂=90

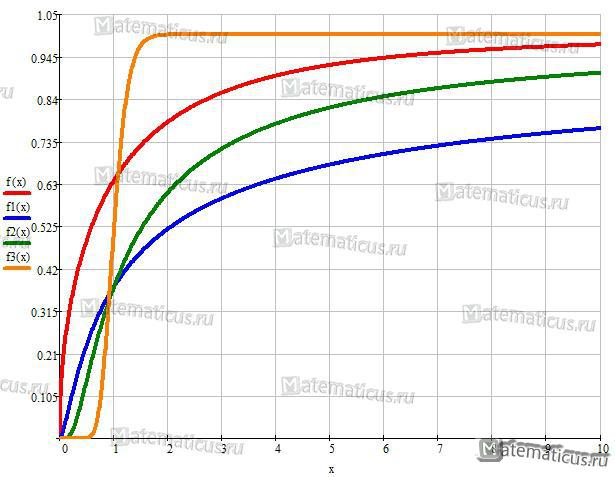
График функции вероятности при k₁=1 и k₂=5, k₁=1 и k₂=4, k₁=90 и k₂=2, k₁=90 и k₂=90

При n→∞ распределение Фишера-Снедекора стремится к нормальному закону распределения СВ.

Математическое ожидание:

M=k₂/(k₂-2), при k₂>2

Дисперсия равна:

$D = \frac{{2k_2^2\left( {{k_1} + {k_2} — 2} \right)}}{{{k_1}{{\left( {{k_2} — 2} \right)}^2}\left( {{k_2} — 4} \right)}}$ при k₂>4

Формула для определения моды:

${M_0} = \frac{{({k_1} — 2){k_2}}}{{2k_1^2 + {k_2}}}$

F-распределение применяется для сравнение двух оценок дисперсий и более, для проверки гипотез в регрессионном анализе.