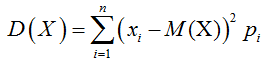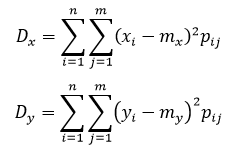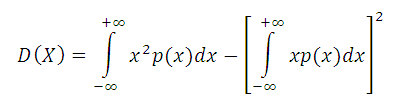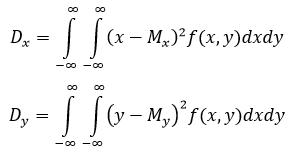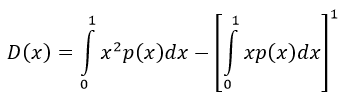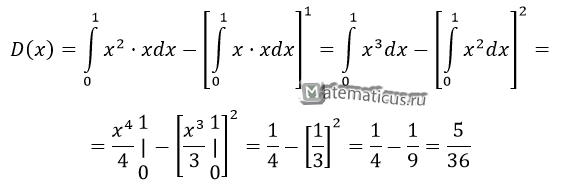Дисперсией случайной величины (СВ) называется математическое ожидание квадрата отклонения значений X от ее среднего значения.
Другое определение, дисперсия СВ — это мера разброса значений случайной величины X вокруг её математического ожидания.
Обозначение: D[X], D(X), DX
Формула дисперсии для дискретной случайной величины X:
D(X)=M(X2)-M2(X)
или
Формула дисперсии для двух независимых дискретных случайных величин:
где M(X) — математическое ожидание
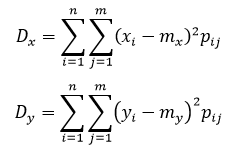
Х — дискретная случайная величина
Формула дисперсии для непрерывной случайной величины X: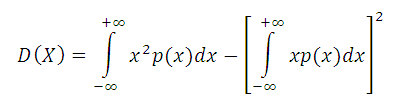
формула дисперсии для двух независимых непрерывных случайных величин:
Дисперсия показывает степень рассеивания случайной величины (числовая характеристика рассеивания, оценка разброса).
Дисперсия числа появлений событий A в n независимых испытаниях вычисляется по формуле:
D(X) = n⋅p⋅q
где
р — одинаковая вероятность появления события A в каждом испытании (опыте);
q = 1-p — вероятность не появления события A.
Пример 1
Найти дисперсию дискретной случайной величины с законом распределения:
| X | 1 | 2 | 3 | 4 |
| P | 0.3 | 0.2 | 0.4 | 0.1 |
Решение
Найдем математическое ожидание М(Х):
М(Х)=1⋅0,3+2⋅0,2+3⋅0,4+4⋅0,1= 2.3
Закон распределения случайной величины для квадрата значений X2 в виде таблицы:
| X | 1 | 4 | 9 | 16 |
| P | 0.3 | 0.2 | 0.4 | 0.1 |
Вычислим дисперсию для дискретной СВ:
M(X2) = 1⋅0,3+4⋅0,2+9⋅0,4+16⋅0,1=
=0,3+0,8+3,6+1,6=6,3
D(X) = M(X2)-M2(X)=6,3-(2.3)2=6,3-5,29=1.01
Пример 2
Найти дисперсию непрерывной случайной величины в интервале (0, 1). Плотность распределения имеет вид:
$p\left( x \right) = \left\{ {\begin{array}{·{20}{c}} {0;x \notin \left( {0;1} \right)} \\ {x;x \in \left( {0;1} \right)} \end{array}} \right.$
Решение
Формула дисперсии для непрерывной СВ имеет вид:
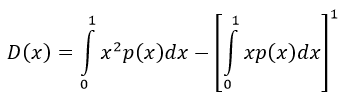
Подставим плотность распределения в формулу, получим решение
Пример 3
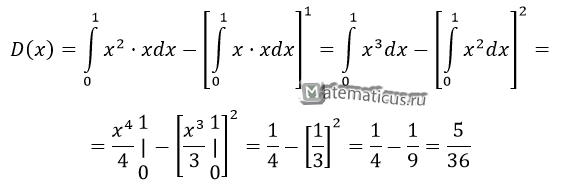
Вероятность отказа элемента в каждом испытании прибора равна 0,7. Требуется найти дисперсию дискретной случайной величины числа отказов прибора в двадцати независимых испытаниях
Решение
Из условия имеем n=20, q=0,7 и р=1-q = 0,3, получаем решение
D(X) = n⋅p⋅q=20⋅0,7⋅0,3=4.2
34822