Нормальный закон распределения

На рисунке ниже показан нормальный закон распределения случайной величины X в виде гистограммы.

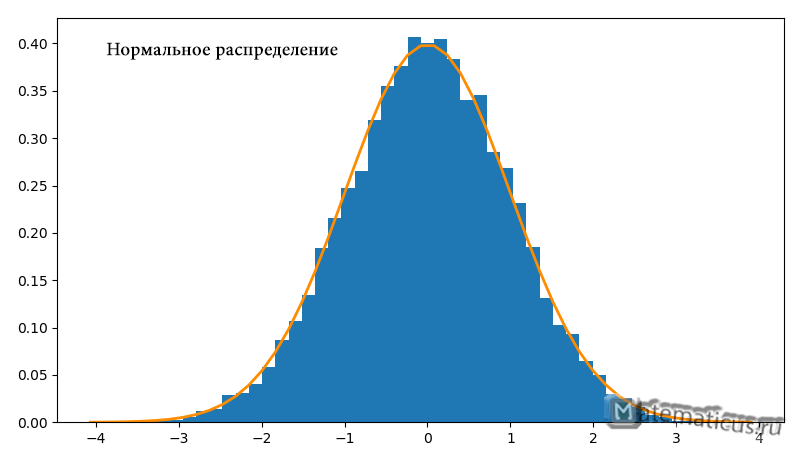
Рисунок 1 — Пример нормального закона распределения

Случайная непрерывная величина X имеет нормальный закон распределения, если ее плотность распределения вероятности имеет выражение:

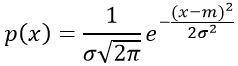
где m, σ —  параметры распределения СВ;
m_xили  m — математическое ожидание случайной величины,
 — среднеквадратичное отклонение от величины a;
σ² — дисперсия.
Формула функции распределения СВ нормального закона определяется по формуле:

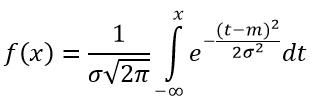
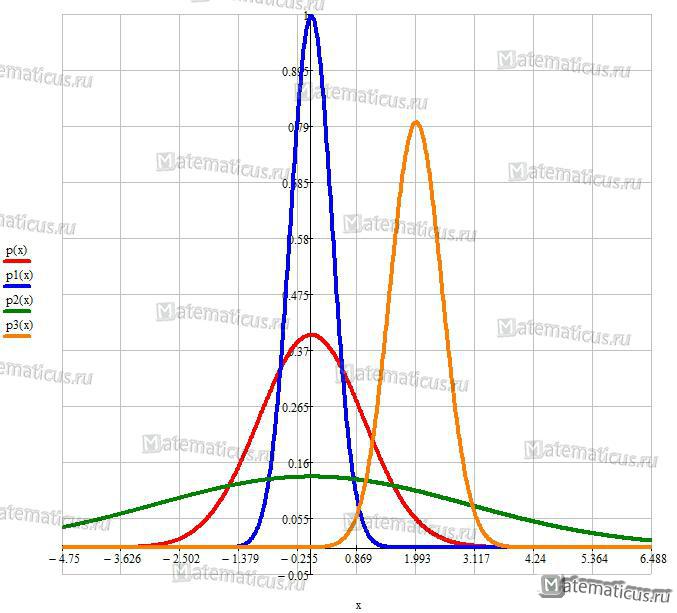
Рисунок 2 — График плотности нормального закона распределения X при m=0 и  σ=1, m=0 и σ=0,4, m=0 и σ=3, m=2 и σ=0,5.

 На рисунке 2 показана функция плотности нормального закона распределения при m=0 и  σ=1;

при m=0 и  σ=0,4 (функция плотности расширяется);
при m=0 и  σ=3 (функция плотности сжимается);
при m=2 и  σ=0,5 (функция плотности смещается вправо на 2 единицы относительно вершины).

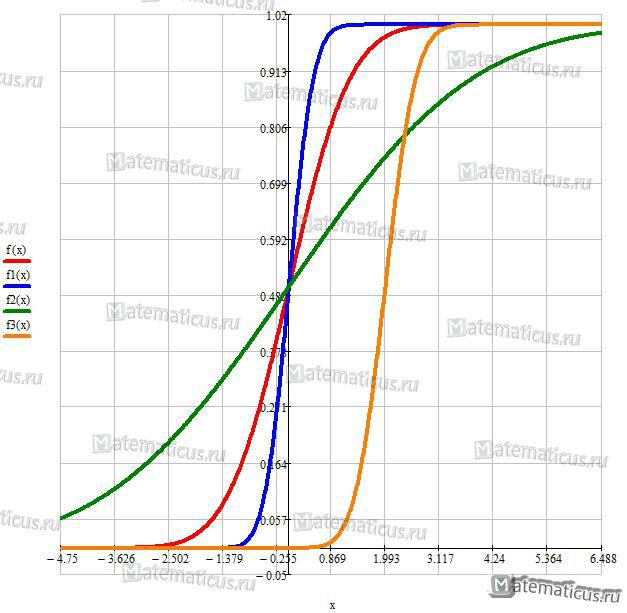
Рисунок 3 — График функции нормального закона распределения X при m=0 и  σ=1, m=0 и σ=0,4, m=0 и σ=3, m=2 и σ=0,5.

При m=0 и  σ=1 на рисунке 2 нормальное распределение СВ называется стандартным нормальным распределением СВ (таблица плотности вероятности нормальной случайной величины), плотность которого равна

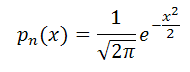
а функция распределения или функция Лапласа (таблица функции Лапласа)

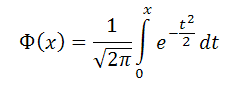
Вероятность попадания в заданный интервал (α; β) распределенной случайной величины по нормальному закону с параметрами a, σ  вычисляется по формуле:

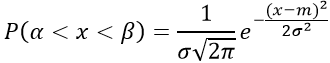
с использованием интеграла вероятности

 

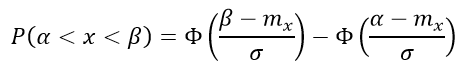
Из этих соотношений легко получить вероятность отклонения распределения случайной величины X от своего математического ожидания m:

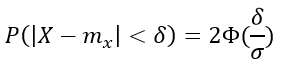
 ,где  δ — величина отклонения.

  Полагая в этой формуле δ=3σ, получаем

P(|X-m_x|<δ)=2·Ф(3)=2⋅0.49865=0.9973

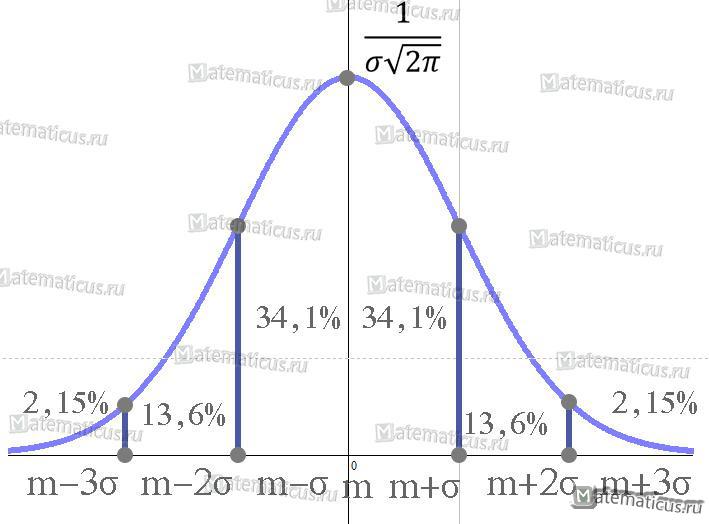
Рисунок 4

Этот правило носит название «правило трех сигм». Таким образом, см. рисунок 4 выше в 2,15+2,15+13,6+13,6+34,1+34,1=99,7% случаях все значения нормального закона распределения случайной величины сосредоточены в интервале (-3σ+m; 3σ+m). Распределение, заданное на бесконечном интервале, может быть рассмотрено на конечном интервале и погрешность при такой замене равна ,примерно, 0,3%.

Замечание
Нормальный закон распределения СВ является основным (базовым), часто встречается на практике и его также называют законом Гаусса.

Используется для построения доверительных интервалов, применяется для моделирования разброса при стрельбе, измерения ошибок и т.д.

При n→∞ биномиальное распределение быстро начинает приближаться к нормальному закону распределения СВ.

---

Пример 1

Математическое ожидание и среднее квадратичес­кое отклонение нормально распределенной случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15, 25).
Решение

$P\left( {15 < x < 25} \right) =$

$={\text{Φ }}\left( {\frac{{25 — 20}}{{5}}} \right) — {\text{Φ }}\left( {\frac{{15 — 20}}{{5}}} \right) = {\text{Φ }}\left( 1 \right) — {\text{Φ}}\left( { — 1} \right)$

Так как функция Ф(х) нечётна:

P(15<x<25)=Ф(1)+Ф(1)=2Ф(1)

По таблице функции Лапласа находим значение Ф(1) =0,3413

Р(15<х<25)=2Ф(1) = 0,6826

---

Пример 2
Случайная величина X распределена нормально с дисперсией 2 и средним квадратическим отклонением 4. Найти вероятность того, что она примет значение в интервале (2, 6).
Решение
D=2 ⇒ σ=$\sqrt 2 $
m_x=4

$P\left( {2 < x < 6} \right) = {\text{Φ }}\left( {\frac{{6 — 4}}{{\sqrt 2 }}} \right) — {\text{Φ }}\left( {\frac{{2 — 4}}{{\sqrt 2 }}} \right)$

$P\left( {2 < x < 6} \right) = {\text{Φ }}\left( {1.41} \right) — {\text{Φ }}\left( { — 1.41} \right)$

По таблице функции Лапласа находим значение Ф(1.41) =0,3413

$P\left( {2 < x < 6} \right) = 2{\text{Φ }}\left( {1.41} \right) = 2 \cdot 0.4207 = 0.8414$

---

Пример 3

На станке изготавливается некоторая деталь. Ее длина представляет собой случайную величину, распределенную по нормальному закону, и имеет среднее значение 20 см и среднее квадратическое отклонение равную 0,2 см. Найти вероятность того, что длина детали будет заключена между 19,7 см и 20.3 см

Решение

$P\left( {19.7 < x < 20.3} \right) =$

$={\text{Φ }}\left( {\frac{{20.3 — 20}}{{0.2}}} \right) — {\text{Φ }}\left( {\frac{{19.7 — 20}}{{0.2}}} \right) = {\text{Φ }}\left( 1 \right) — {\text{Φ}}\left( { — 1} \right)$

P(19.6<x<20.4)=Ф(1)+Ф(1)=2Ф(1)

По таблице функции Лапласа находим значение Ф(1) =0,3413

Р(19,7<х<20,3)=2Ф(1) = 0,6826

---

Пример 4
Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением σ=10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

Решение

P(|X-m_x|<δ)=2·Ф( δ/σ )

Математическое ожидание равно нулю, δ=15, σ=10, тогда

 P(|X|<15)=2·Ф(15/10)=2Ф(1.5)

По таблице функции Лапласа находим значение Ф(1.5) =0,43319

P(|X|<15)=2·Ф(1.5)=0,86638