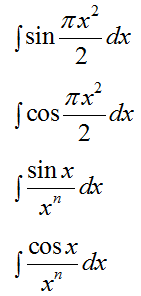Неберущимся интегралом называется такой интеграл, который нельзя выразить через простые функции и данные функции неинтегрируемы и поэтому он неизвестен.
Данные неберущиеся интегралы нельзя найти аналитическим методом, лишь только приближенно, воспользовавшись существующими численными методами вычисления определенных интегралов, например, метод Симпсона, метод трапеций, метод прямоугольников
Список неберущихся интегралов:
- интегральный синус или интеграл Френеля:

- интегральный косинус или интеграл Френеля:
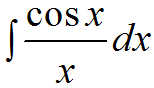
- интегральный логарифм:
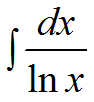
4. неберущиеся эллиптический интеграл первого рода:
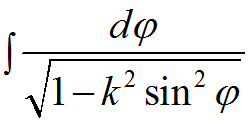 5. неберущиеся интеграл вероятности или Пуассона (данная функция часто применяется в теории вероятностей для вычисления функции Лапласа):
5. неберущиеся интеграл вероятности или Пуассона (данная функция часто применяется в теории вероятностей для вычисления функции Лапласа):
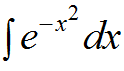
или
$$\int {{e^{ — \frac{{{x^2}}}{2}}}} \,dx$$
6. интегральная экспонента:
$$\int {\frac{{{e^x}}}{x}} \,dx$$
7. интеграл Френеля:
$$\smallint {\bf{sin}}\left( {{{\bf{x}}^{\bf{2}}}} \right){\bf{dx}}$$
8.интеграл Френеля:
$$\smallint {\bf{cos}}\left( {{{\bf{x}}^{\bf{2}}}} \right){\bf{dx}}$$
Дополнительные неберущиеся интегралы Френеля: