Вычисление определенного интеграла методом прямоугольников

Метод  прямоугольников предназначен для вычисления определённого интеграла и относится к приближенному методу вычисления интегралов.
Формулы для нахождения приближенного значения определённого интеграла методом прямоугольников имеют вид:

 

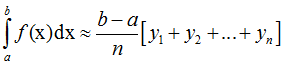
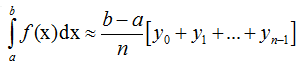
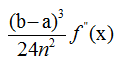
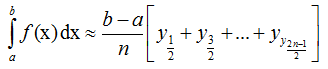
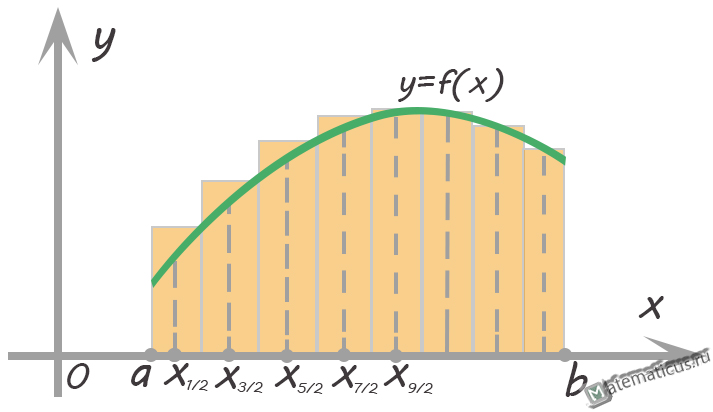
График — метод прямоугольников

Погрешность значения формулы прямоугольников вычисляется по следующему выражению:

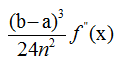
f’’(x) – наибольшее значение производной |f’’(x)|, x(a, b)

---

Пример
Вычислить интеграл численным методом для функции:

$$\int\limits_0^1 {{e^x}dx} $$

Решение
Найдём значения x в диапазоне от 0 до 1 с шагом 0.1, всего 10 значений
x_1/2=0,05
x_3/2=0,15
x_5/2=0,25
x_7/2=0,35
x_9/2=0,45
x_11/2=0,55
x_13/2=0,65
x_15/2=0,75
x_17/2=0,85
x_19/2=0,95
Получившиеся значения подставим в функцию e^x, получаем
y_1/2=1,051271096
y_3/2=1,161834243
y_5/2=1,284025417
y_7/2=1,419067549
y_9/2=1,568312185
y_11/2=1,733253018
y_13/2=1,915540829
y_15/2=2,117000017
y_17/2=2,339646852
y_19/2=2,585709659
Подставляя в формулу прямоугольников, найдём решения определённого интеграла:

$$I \approx \frac{{b — a}}{n}\sum y = \frac{{1 — 0}}{{10}}17,17566 = 1,717566$$

Погрешность равна 0,0007157

Для сравнения точности методов вычисления определённого интеграла см. решения этого же итеграла методом Симпсона и методом трапеций.
Точное аналитическое решение данного определённого интеграла см.здесь