Геометрическое определение вероятности применимо для несовместных событий, в которых число равновозможных исходов бесконечно, например, попадания точки на участок отрезка, плоскости, пространства, объёма.
Общая формула для определения геометрической вероятности:
$P\left( A \right) = \frac{{mes\left( g \right)}}{{mes\left( G \right)}}$
Отношение меры области g, благоприятствующей событию А, к мере всей области G.
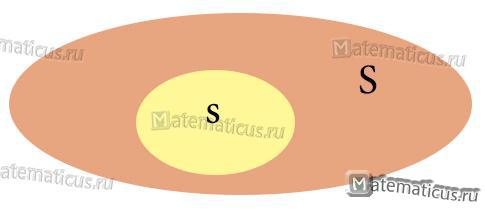
Формула геометрической вероятности попадания точки на участок отрезка L для одномерного пространства равна:
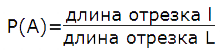
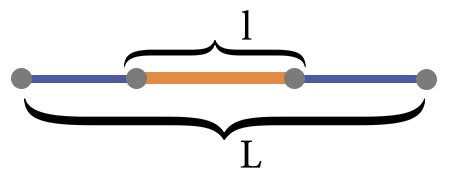
Формула геометрической вероятности попадания точки в область пространства S для фигур в двухмерном пространстве равна:
![]()
Формула геометрической вероятности попадания точки в заданный объём для фигур в трёхмерном пространстве V равна:
![]()

Пример 1
Решение
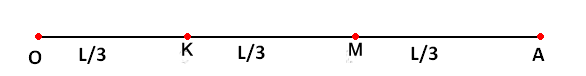

Пример 2
Решение
Аналогично первому примеру, вероятность равна:
P(A)=l/L=10/20=1/2
Пример 3
В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.
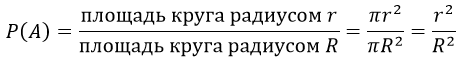
Пример 4
Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры
Решение
P(A)=0.5·πr2/πr2=0.5
Пример 5
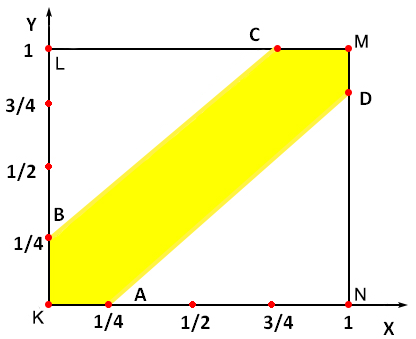
Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 1/4 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).
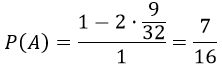
Пример 6
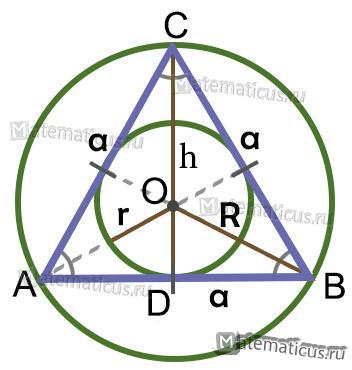
Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг:
а) квадрата;
б) правильного треугольника.
Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.
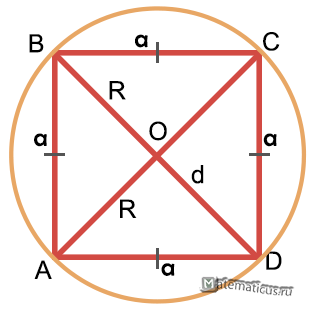
$AB = \frac{{AC}}{{\sqrt 2 }} = \frac{{2R}}{{\sqrt 2 }} = \sqrt 2 R$
${S_{ABCD}} = A{B^2} = {\left( {\sqrt 2 R} \right)^2} = 2{R^2}$
${S_{ABCD}} = 2 {R^2}$
Sкруга=πR2
$$P\left( A \right) = \frac{{2 \cdot {R^2}}}{{\pi \cdot {R^2}}} = \frac{2}{\pi }$$

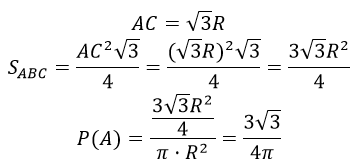
Еще пример, задача Бюффона о бросании иглы
