Задача Бюффона о бросании иглы
Метод Бюффона основан на методе Монте-Карло и заключается в бросании иглы на плоскость, расчерченную на расстоянии друг от друга параллельными прямыми. Этот метод также применяется для вычисления числа π. Чем больше количества повторений опыта, тем точнее будет результат.
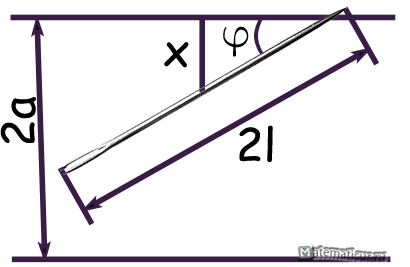
Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросают иглу длины 2l (2l≤2а), φ – угол. Найти вероятность того, что игла пересечет какую-нибудь прямую.
Решение
Графически задачу Бюффона можно представить следующем образом:
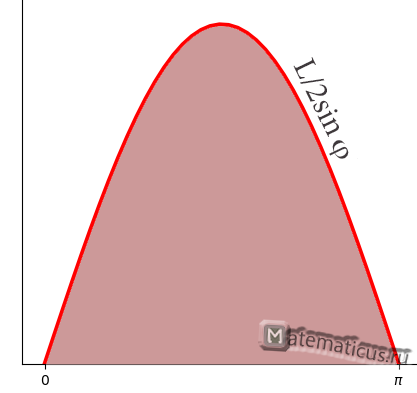
Найдем вероятность через вычисления интеграла:
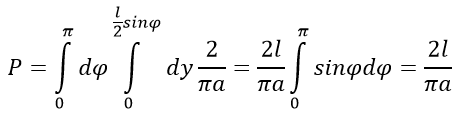
Экспериментально по методу Монте-Карло вероятность определяется по формуле:
P≈[кол-во бросаний]/[кол-во пересечений]
Число π приближенно можно определить по методу Монте-Карло по формуле:
π≈2L*[кол-во бросаний]/a*[кол-во пересечений]
a — расстояние между линиями.
Если мы сделаем предположение, что длина иглы равна расстоянию между линиями, то выражение определяется по формуле:
π≈2*[кол-во бросаний]/[кол-во пересечений]
В практических вычислений вероятности также используют условие, что параллельные линии находятся друг от друга на расстояние двух длин иглы

Представим себе, что к концу иглы прикреплена тонкая окружность диаметром 2a. Будем при
каждом броске этой фигуры отмечать на ней точки пересечения с линиями. После множества
бросков фигура — игла с прикреплённой окружностью, покроется множеством точек. Поскольку
процесс случайный, точки лягут равномерно по всей фигуре. Следовательно, соотношение
числа точек на игле и на окружности пропорционально их длинам, т. е. 2l/(pi*2a). Но окружность,
диаметр которой равен расстоянию между линиями, при каждом броске пересекает линию дважды, либо касается двух соседних линий, и после N бросков на ней будет 2N точек,
а на игле 2Nl/(pi*a).