Числовые характеристики случайных величин

Перечислим основные характеристики случайных величин:
— математическое ожидание (характеризует среднее значение);
— дисперсия;
— среднеквадратическое отклонение;
— медиана случайной величины;
— мода случайной величины;
— начальный момент;
— центральный момент;
— аcсимметрия;
— эксцесс;
— квантиль уровня.

Математическое ожидание для непрерывной и дискретной случайной величины
Дисперсия для непрерывной и дискретной случайной величины
Среднеквадратическое отклонение случайной величины

Медиана случайной величины — это такое значение случайной величины X, при котором X=Me и  Me разделяет область значений на две части, вероятности попадания в любую из данных областей равновероятны, то есть выполняется условие:

p(X<Me)=p(X>Me)

F(Me)=0.5

Модой для дискретной случайной величины называют такое значение, которое наиболее вероятно.

Модой для непрерывной случайной величины называют наибольшее значение (точка локального максимума) плотности вероятности.

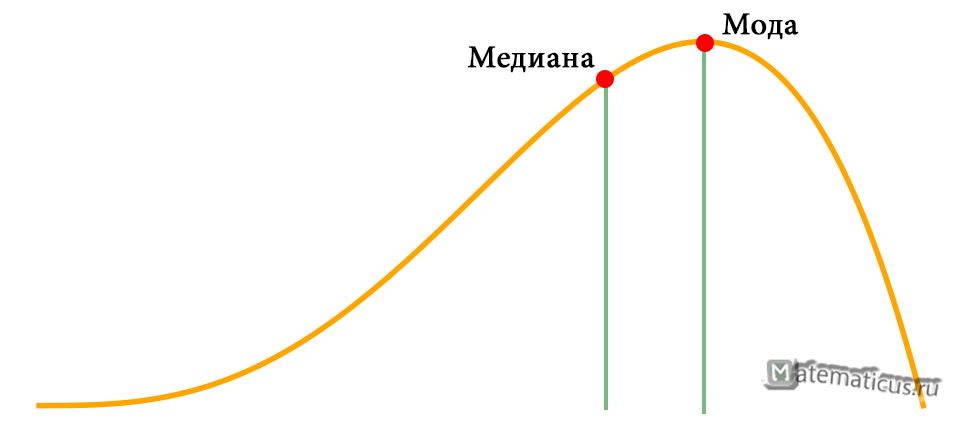
Мода и медиана на графике  

Начальным моментом порядка k случайной величины X называется математическое ожидание величины Х^k и определяется равенством:

ν_k=M(Х^k)

Формула начального момента для непрерывной случайной величины:

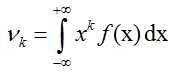
Формула начального момента для дискретной случайной величины:

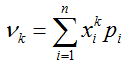
Центральным моментом порядка k случайной величины X называется математическое ожидание величины (X-M(Х))^k и определяется равенством:

μ_k=M[X-M(Х)]^k

Формула центрального момента для непрерывной случайной величины:

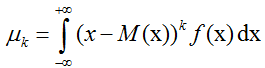
Формула центрального момента для дискретной случайной величины: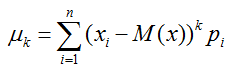

Центральный момент первого порядка случайной величины X равен нулю, то есть

μ₁=0

Центральный момент второго порядка случайной величины X равен дисперсии, то есть

μ₂=D(x)

μ₂=ν₂–(ν₁)²

Центральный момент третьего порядка случайной величины X характеризует асимметрию и определяется равенством:

μ₃=ν₃–3ν₂ν₁+2(ν₁)²

Центральный момент четвёртого порядка случайной величины X характеризует эксцесс и  равен:

μ₄=ν₄–4ν₃ν₁+6ν₂(ν₁)²–3(ν₁)⁴

Асимметрия характеризует меру сдвига распределения случайной величины в левую или правую часть и находится по формуле: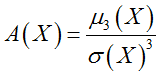

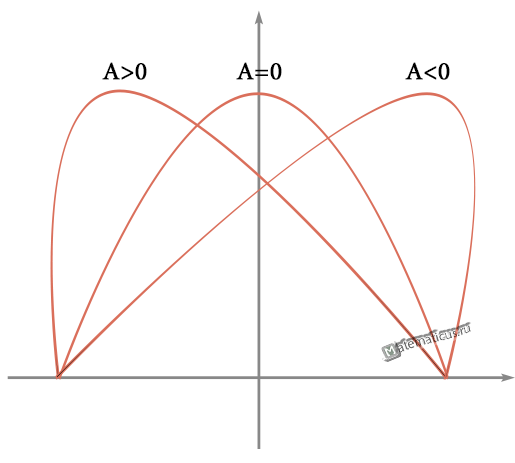
График — асимметрия  

Эксцесс — характеристика вогнутости и выпуклости распределения случайной величины и вычисляется по формуле:

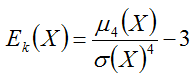
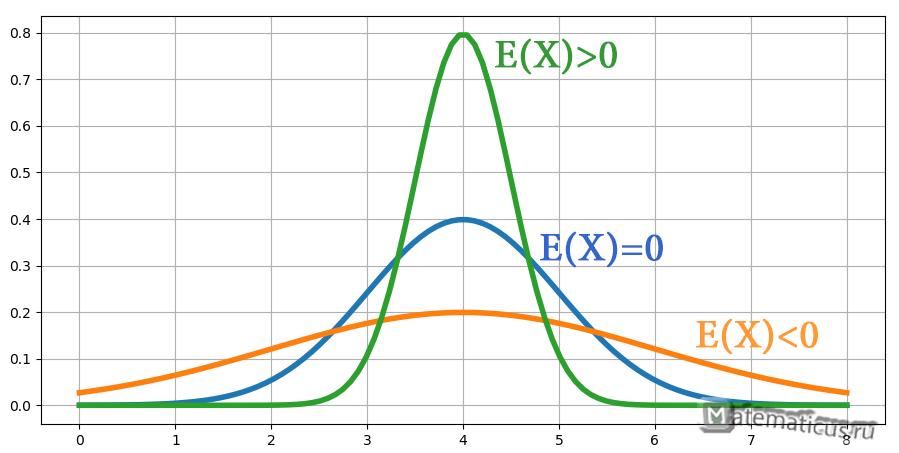
График значений коэффициента эксцесса

Квантилем уровня p называют такое значение случайной величины x_p которое удовлетворяет условие:

F(x_p)=p