Биномиальный закон распределения случайной величины определяется при помощи формулы Бернулли:
Рассмотрим примеры применения формулы Бернулли для построения биномиальных законов распределения дискретной случайной величины X.
Пример 1
Написать биномиальный закон распределения дискретной случайной величины X –числа появлений «герба» при двух бросаниях монеты.
Решение
При бросании монеты вероятность выпадения «герба» равна 0.5, а «решки» q=1–p=1-0.5=0.5
Также случайная величина X — числа появлении «герба» принимает значения: 0, 1, 2
Найдём значения случайной величины X:
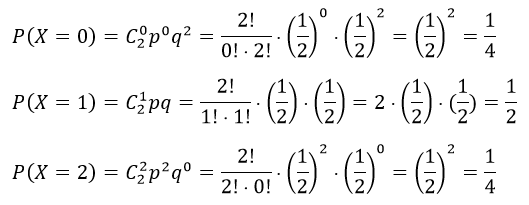
и в виде таблицы составим биномиальный закон распределения СВ X:
| X | 0 | 1 | 2 |
| P | 0.25 | 0.5 | 0.25 |
Пример 2
Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X — числа выпадений четного числа очков на двух игральных костях.
Решение
По условию задачи, кость бросается два раза — составим в виде таблицы всевозможные комбинации выпадения четного и нечетного числа очков
| Первая кость | Вторая кость |
| Четное число очков | Четное число очков |
| Четное число очков | Нечетное число очков |
| Нечетное число очков | Четное число очков |
| Нечетное число очков | Нечетное число очков |
В соответствии с таблицей, из четырёх комбинаций числа выпадений четного числа равна единице, следовательно, р=1/4=0.25, а не выпадения — q=1–p=1-0.25=0.75
Дискретная случайная величина X принимает следующие значения: 0, 1, 2
По формуле Бернулли составим биномиальный закон распределения СВ X:
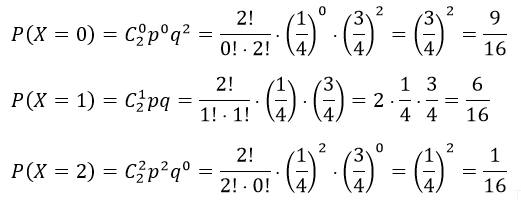Сведём данные биномиального закона распределения X в таблицу:
| X | 0 | 1 | 2 |
| P | 0.5625 | 0.375 | 0.0625 |
Пример 3
В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X — числа нестандартных деталей среди четырех отобранных.
Решение
Из условия задачи p = 0.1, q=1–р=0.9
Возможные варианты значений СВ X: 0, 1, 2, 3, 4
По формуле Бернулли имеем:
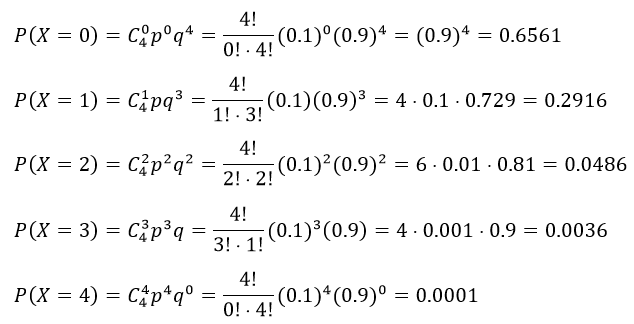Ряд распределения по биномиальному закону распределения случайной величины X имеет вид:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.6561 | 0.2916 | 0.0486 | 0.0036 | 0.0001 |
Пример 4
Студенты техникума вышли на посадку цветов. Всхожесть семян цветов оценивается вероятностью 0,6. Какова вероятность, что из 10 посеянных цветов взойдет 5?
Решение
${P_{10}}\left( 5 \right) = P\left( {X = 5} \right) = C_{10}^5{0,6^5}{0,4^{10 — 5}} ≈0,2$
Пример 5
В библиотеке 50000 книг. Из них 1000 на иностранных языках. Студент взял в библиотеке 20 книг. Какова вероятность, что среди них 5 на иностранных языках?
Решение
p=1000/50000=0,02
q=1−0,02=0,98
$P=\frac{20!}{5!15!}·{0,02^5}·{0,98^{15}} ≈3,66·10^{-5}$
24761