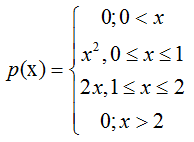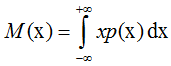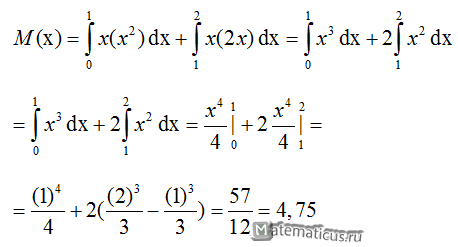Математическое ожидание для непрерывной и дискретной случайной величины

Математическое ожидание (среднее значение) случайной величины X характеризует центр рассеяния случайной величины X.

Обозначение: М[Х], М(Х), M_X, m

Формула для определения математического ожидания дискретной случайной величины X:

  M(X)=x₁⋅p₁+x₂⋅p₂+…+x_n⋅p_n

или

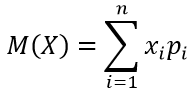
Формула математического ожидания двух независимых дискретных случайных величин: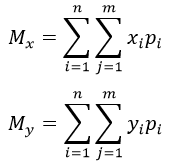

Формула для определения математического ожидания непрерывной случайной величины X:

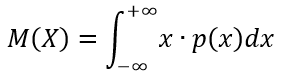
Формула математического ожидания двух независимых непрерывных случайных величин X:

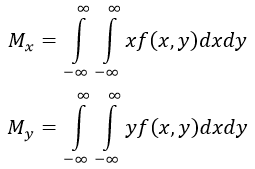
где p(x) — плотность распределения

Замечание

Для непрерывной случайной величины X математическое ожидание может и не существовать.

Решение

Подставляя в формулу выше, находим математическое ожидание M(x):

  М(Х)=3*0,3+4*0,4+5*0,2=

=0,9+1,6+0,5=3,1

---

Пример 2

Найти математическое ожидание для непрерывной случайной величины X, которая имеет плотность распределения в виде следующей функции

 

Решение

Для решения данного примера воспользуемся формулой для вычисления математического ожидания непрерывной случайной величины

Итак, подставляя в формулы, получаем решения