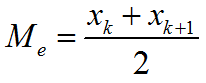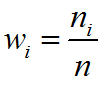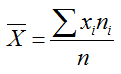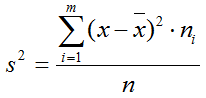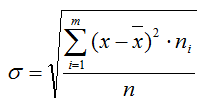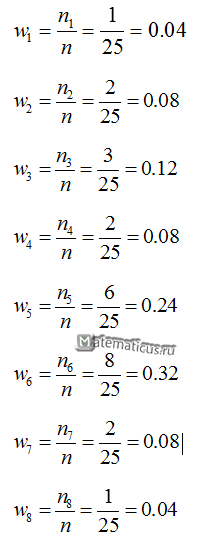Генеральная совокупность представляет собой всю совокупность исследуемых объектов (например население города, ) и обозначается N.
Выборка — это ограниченное по количество объектов n, извлечённых случайным образом из генеральной совокупности.
Вариантами называются значения выборки x1, x2,…,xi, а частоты — n1, n2,…,ni
Если варианты представлены в упорядоченном отсортированном виде, обычно от минимального значения к максимальному, то такие варианты называются вариационным рядом.
Представим вариационный ряд в виде таблицы:
| Xi |
x1 |
x2 |
…… |
xn |
| ni |
n1 |
n2 |
…… |
nn |
Размах выборки — это разность между минимальным и максимальным значениями выборки и вычисляется по формуле:
Мода М0 в статистике называется варианта, которая чаще всего встречается в данной выборки и имеет наибольшую частоту (повторяемость).
Медиана Me — это варианта, находящиеся в середине вариационного ряда, делящая его пополам.
Формула для вычисления медианы нечетного вариационного ряда n=2k+1:
Me=xk+1
Формула для определения медианы четного вариационного ряда n=2k:
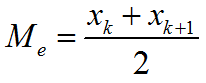
Относительной wi частотой называется отношение частоты к объёму выборки и определяется по формуле
Примечание
Сумма относительных частот равна единице
∑wi=1
Таблица распределения относительных частот имеет вид:
В обувном магазине
Статистика покупки обуви в магазине за один день в соответствии с размерами равна:
42, 41, 43, 40, 39, 44, 38, 42, 41, 39, 43, 41, 42, 37, 42, 41, 39, 42, 42, 41, 40, 41, 42, 38, 42
Требуется найти моду, медиану, размах выборки, построить таблицу распределения частот и относительных частот.
Решение
Отсортируем выборку и запишем вариационный ряд:
37, 38, 38, 39, 39, 39, 40, 40, 41, 41, 41, 41, 41, 41, 42, 42, 42, 42, 42, 42, 42, 42, 43, 43, 44
Обозначим варианты и их частоты:
x1=37, х2=38, х3=39, х4=40, х5=41, х6=42, х7=43 и х8=44
n1=1, n2=2, n3=3, n4=2, n5=6, n6=8, n7=2 и n8=1
Объем выборки равен
n=1+2+3+2+6+8+2+1=25
Размах выборки равен:
R=х8-х1=44–37=7
Найдем моду, наибольшая частота в вариационном ряде равна n6=8, тогда мода равна
М0=42
Число вариант восемь, то есть четно, следовательно медиана равна:
$${M_e} = \frac{{{x_4} + {x_5}}}{2} = \frac{{40 + 41}}{2} = 40.5$$
Вычислим относительные частоты:
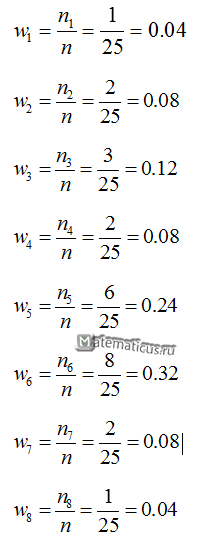
Составим таблицу частот
| Xi |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
| ni |
1 |
2 |
3 |
2 |
6 |
8 |
2 |
1 |
и таблицу относительных частот:
| Xi |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
| ni |
0.04 |
0.08 |
0.12 |
0.08 |
0.24 |
0.32 |
0.08 |
0.04 |
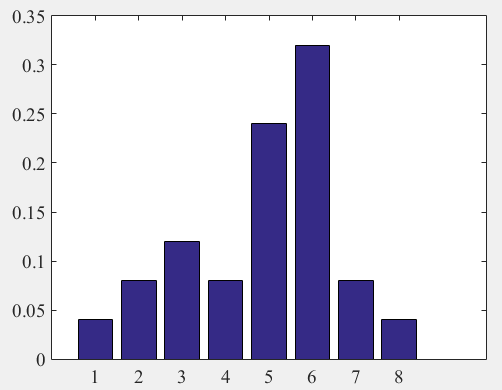
Гистограмма относительных частот