Двухпараметрический закон Вейбулла характеризует распределение непрерывной СВ, которая принимает только положительные значения.
Функция плотности распределения случайной величины Вейбулла находится по формуле:
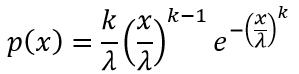
Интегральная функция распределения определяется выражением:
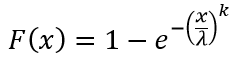
Переменная x часто рассматривается как наработка.
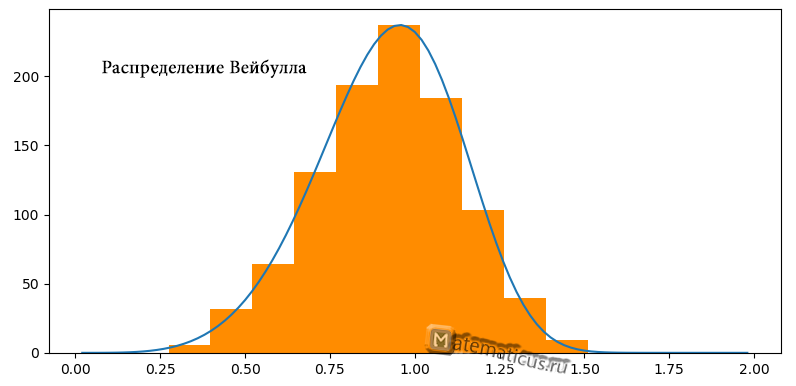
Распределение Вейбулла в виде гистограммы
Параметры распределения:
λ — масштаба распределения распределения случайной величины Вейбулла;
k — параметр формы распределения СВ Вейбулла.
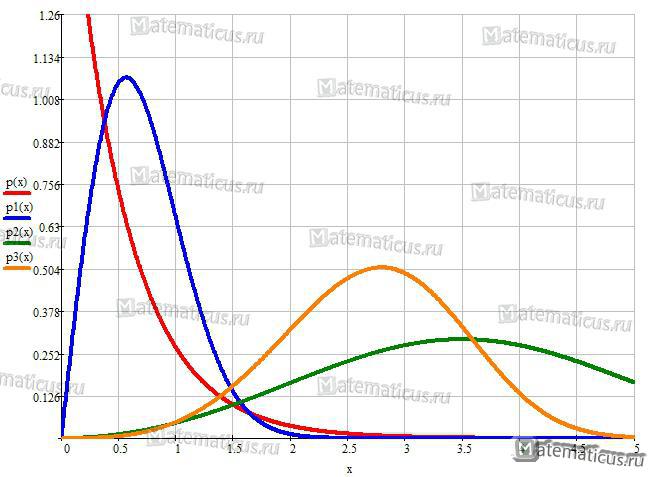
График плотности распределения случайной величины Вейбулла при k=1 и λ=0.5, k=2 и λ=0.8, k=3 и λ=4, k=4 и λ=3
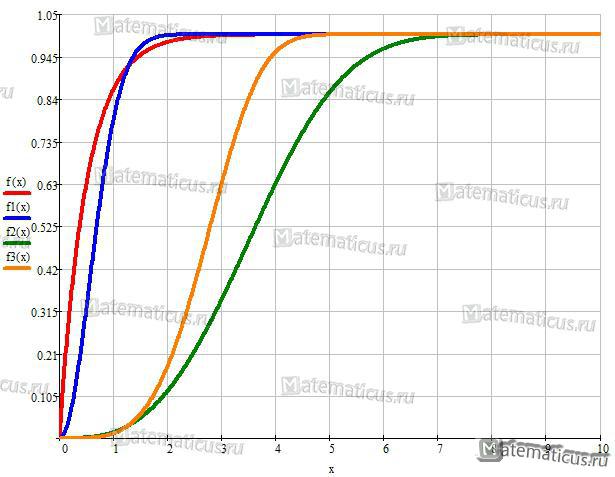
График функции распределения случайной величины Вейбулла при k=1 и λ=0.5, k=2 и λ=0.8, k=3 и λ=4, k=4 и λ=3
Обратная функция распределения Вейбулла вычисляется по формуле:
F-1(x)=-λ[ln(1-x)]1/k
При k=1 закон распределения Вейбулла переходит в показательный (экспоненциальный) закон распределения.
При k=2 закон распределения Вейбулла превращается в закон распределения Рэлея.
Распределение Вейбулла применяется в теории надежности (анализ отказов деталей:
— при k>1 — старение, то есть частота отказов увеличивается с течением времени;
— при k<1 — эксплуатация, то есть частота отказов уменьшается с течением времени;
— при k=1 — интенсивность отказов постоянна во времени.
Распределение Вейбулла применяют при прогнозировании времени до отказа технической системы, для непрерывных показателей, погоды (скорость ветра подчиняется этому закону) и т.д.
