Показательный (экспоненциальный) закон распределения

Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если её плотность вероятности имеет вид:

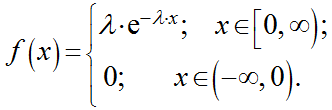
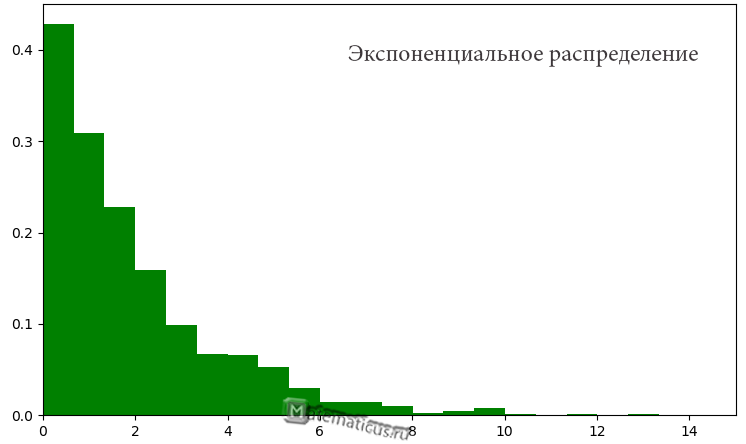
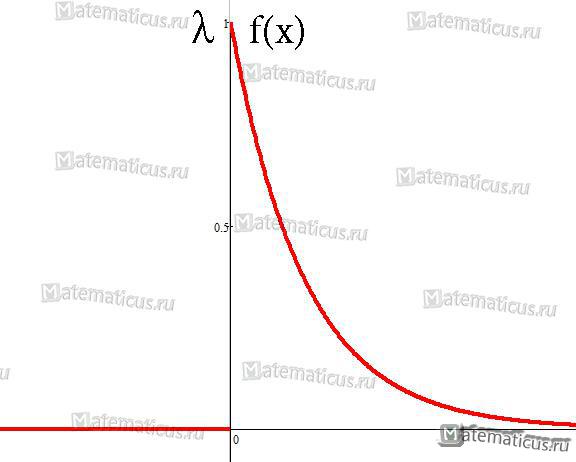
График плотности распределения случайной величины по показательному (экспоненциальному) закону

Функция распределения F(X) случайной величины X, распределенной по показательному закону,  выражается формулой:

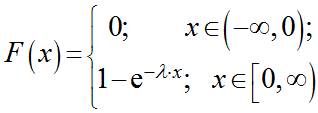
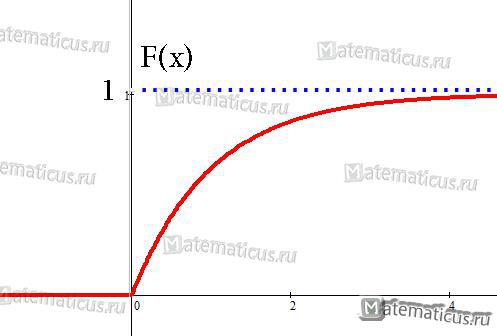
График функции распределения случайной величины по показательному (экспоненциальному) закону

λ — параметр распределения.

Математическое ожидание равно:

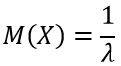
Дисперсия равна:

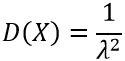
Среднеквадратическое отклонение (СКО) σ(X) равно:

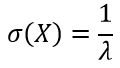
Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), находится по формуле:

P(a<X<b)=e^−λa−e^−λb

Вероятность безотказной работы определяется по формуле:

$P(t)=e^{-\lambda t}$

а вероятность отказа (или интенсивность отказов) равна

$F(t)=1-e^{-\lambda t}$

Интенсивность отказа:

$\lambda (t)=\lambda=const$

Среднее время безотказной работы T₀:

$T_0=\frac{1}{\lambda}$

Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии и т. д. Пример, устройство после включения ломается через короткий промежуток времени.

---

Пример

Случайная величина X – время работы лампы накаливания.  Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.

Решение

В соответствии с  условием задачи, математическое ожидание M(x) случайной величины X равно 400 часам, отсюда следует, что

\[\lambda  = \frac{1}{{400}}\]

Подставляя в формулу выше, получаем вероятность

\[P(T \geqslant 800) = 1 — P(T < 800) = 1 — F(800) = \]

\[=1 — (1 — {e^{ — \;\frac{1}{{400}} \cdot 800}}) == {e^{ — \;\frac{{800}}{{400}}}} = {e^{ — 2}} \approx 0,137\]