Локальная теорема Муавра – Лапласа
Если вероятность p появления события в испытании равна (0<p<1), тогда из этого следует при n→∞.
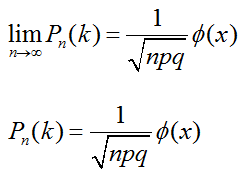
где функция Гаусса находится по формуле:
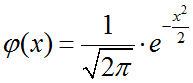
$$x = \frac{{k — np}}{{\sqrt {npq} }}$$
Формулу применяют при неограниченном возрастании количества испытаний. Эта формула является заменой сложной формулы Бернулли при больших значениях n.
При отрицательных значений аргумента применяют ту же таблицу, что и для положительных. Это связано с тем, что функция четна, т.е.
$$\varphi ( — x) = \varphi (x)$$
Пример
Найти вероятность того, что событие – нажатие на тормоз наступит 80 раз на 700 – километровой дороги, если вероятность нажатие на тормоз на каждом километре равна 0,1
Решение
Из условия получаем
N=700
k=80
p=0,1
q=0,9
По асимптотической формуле Лапласа находим
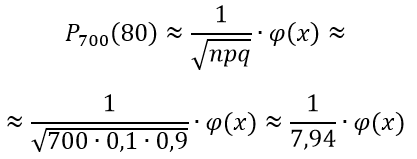
Находим x

Значения Φ находим по таблице Гаусса здесь.
φ(1,26)=0,18
Находим искомую вероятность
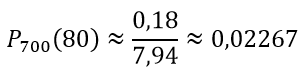

Неправильно решена задача, проверяйте перед публикацией , ответ там 0.023
Спасибо Вам за внимательность! Исправили ход решения задачи.