Общая схема исследования графика функции

Схема исследования функции

1. Найти область значений E(f) и область определения D(f) функции;
2. Определить четность или нечетность функции, периодичность функции;
3. Найти точки пересечения графика функции с осями координат;
4. Нахождение  вертикальной, горизонтальной и наклонной асимптоты;
5. Определение критических точек, экстремумов функции, наибольшее и наименьшее значение, интервалы монотонности функции — возрастания и убывания функции;
6. Определение интервалов вогнутости, выпуклости, точек разрыва и перегиба функции;
7. Построить график исходной функции (построить график, касательную и её производную онлайн).

---

Пример
Исследовать функцию и построить график функции

$y = \frac{{{x^2}}}{{x — 2}}$

Решение
1.

D(f)=(−∞;2)∪(2;+∞)

E(f)=(−∞;0)∪(8;+∞)

2.
Функция ни четная и ни нечётная, непериодическая

${\rm{f}}\left( { — {\rm{x}}} \right) = \frac{{{{( — x)}^2}}}{{ — x — 2}} = \frac{{{x^2}}}{{ — x — 2}}$

3.
Ox: ${\rm{y}} = \frac{{{x^2}}}{{x — 2}} = 0$, x=0 точка (0;0)
Oy: x=0, y=0 точка (0;0)
4.
Так как

$\mathop {{\rm{lim}}}\limits_{x \to + 2} \frac{{{x^2}}}{{x — 2}} = + \infty $

$\mathop {{\rm{lim}}}\limits_{x \to — 2} \frac{{{x^2}}}{{x — 2}} = — \infty $

следовательно
x = 2 — вертикальная асимптота
Уравнение наклонной асимптоты (как определить её, пример см. здесь)

y=x+2

5.
Вычисляем первую производную функции:

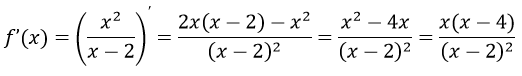
Находим критические точки:

$\frac{{x\left( {x — 4} \right)}}{{{{\left( {x — 2} \right)}^2}}} = 0$

отсюда получаем корни уравнения
x=2, x=4, x=0
Исследуем знак производной на интервалах

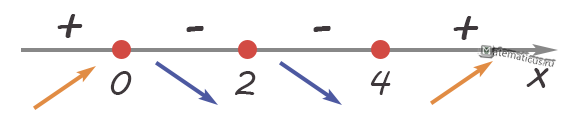
Функция возрастает при

$x∈\left( { — \infty ;0} \right)\mathop \cup \nolimits \left( {4; + \infty } \right)$

Функция  убывает при

$x∈\left( {0;2} \right)\mathop \cup \nolimits \left( {2;4} \right)$

Функция имеет максимум при f(0)=0
Функция имеет минимум при 

$f(4) = \frac{{{4^2}}}{{(4 — 2)}} = 8$

6.
Вычисляем вторую производную

${\rm{f}}\left( {\rm{x}} \right) = \left( {\frac{{{x^2} — 4x}}{{{{\left( {x — 2} \right)}^2}}}} \right){\rm{}} = \frac{{\left( {2x — 4} \right){{\left( {x — 2} \right)}^2} — \left( {{x^2} — 4x} \right)\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}} = \frac{{4\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}}$

Приравниваем к нулю и находим критические точки:

$\frac{{4\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}} = 0$

x=2 точка разрыва функции
Функция выпукла вверх при x∈(−∞;2)
Функция выпукла вниз при x∈(2;+∞)
Точки перегиба нет.
7. 

Строим график функции
Онлайн график можно построить здесь.

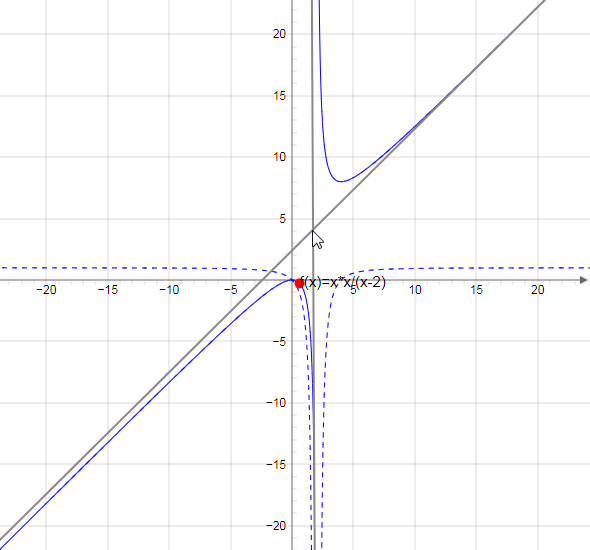
Пунктирной линией показана производная функции.