Метод множителей Лагранжа Найти экстремум функции

Метод множителей Лагранжа заключается в составлении функции Лагранжа, вида

L(x₁,x₂..x_n,λ)=f(x₁,x₂..x_n)+λ·∑g(x₁,x₂..x_n)

λ — неопределённый множителей Лагранжа

Составляется уравнение в соответствии с частными производными и находятся критические точки. Условия экстремума.

∂L/∂x₁=0

∂L/∂x₂=0

…………..

∂L/∂x_n=0

∂L/∂λ=0

Определяется условный экстремум функции.

Характер условного экстремума определяется из знака второго дифференциала функции Лагранжа

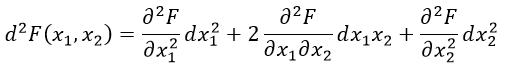
При d²F>0 — функция имеет условный минимум;

При d²F<0 — функция имеет условный максимум.

Также в стационарной точки функция должна быть положительна, то есть:

---

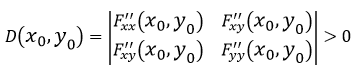
Пример

Определить экстремумы функции

f(x,y)=x+y, если xy=100, x>0, y>0

Решение

Запишем функцию Лагранжа

L(x,y,λ)=x+y+λ(xy−100)

и исследуем ее

Найдем частные производные от функции Лагранжа и составим систему уравнений на основе метода Лагранжа

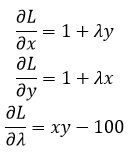
Приравниваем к нулю и решаем систему уравнений

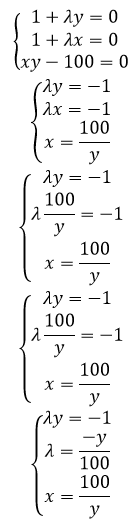
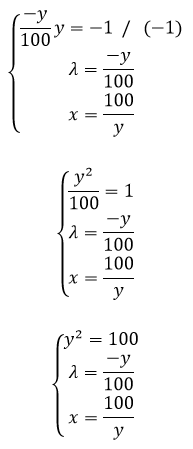
Так как в системе уравнений несколько корней, разбиваем на две системы уравнений

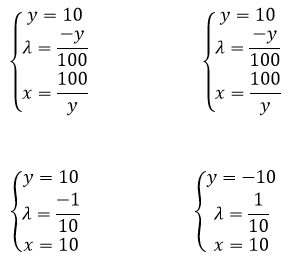
В итоги получаем две критические точки, но так как по условию x>0, y>0, следовательно, оптимальной точкой на основе метода множителей Лагранжа будет точка с координатами (10;10) — точка условного экстремума функции, то есть

f(10,10)=20

Так как d²F>0 и D(x0;y0)>0, следовательно данная точка является условным минимум