Вогнутость и выпуклость функции
Выпуклой функцией y=f(x) называется такая функция, у которой вторая производная на данном промежутке принимает отрицательные значения, то есть:
f ′′(x)<0
Вогнутой функцией y=f(x) называется такая функция, у которой вторая производная на данном промежутке принимает положительные значения, то есть:
f ′′(x)>0
На графике 1 показана выпуклость функции, а на графике 2 показана вогнутость функции

График 1 — Функция находится ниже касательных к графику функций
График 2 — Функция находится выше касательных к графику функций
Точки перегиба функции
Точками перегиба графика непрерывной функции называют такие точки, у которых при f ′′(x) изменяется знак при переходе аргумента через критическую точку и третья производная не равна нулю.
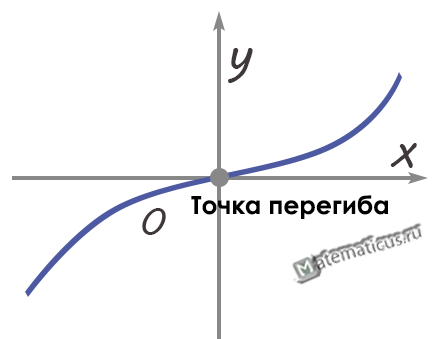
Здесь x0 — точка перегиба
Пример
Найдите точки перегиба для функции:
$y=\frac{3}{4}x^{4}-\frac{1}{2}x^{2}+x-3$
Функция имеет график
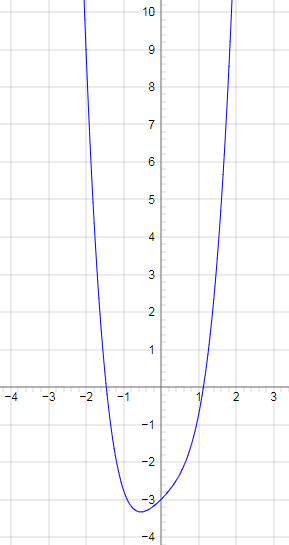
Решение
Первая производная функции равна:
$y^{′}=3x^{3}-x+1$
Вторая производная функции равна:
$y^{′′}=9x^{2}-1$
Третья производная функции равна:
$y^{′′′}=18x$ больше нуля.
Из функции $y^{»}=9x^{2}-1$ найдем точки перегиба
$9x^{2}-1=0$ отсюда $x=\pm\frac{1}{3}$
График функции с точками перегиба

