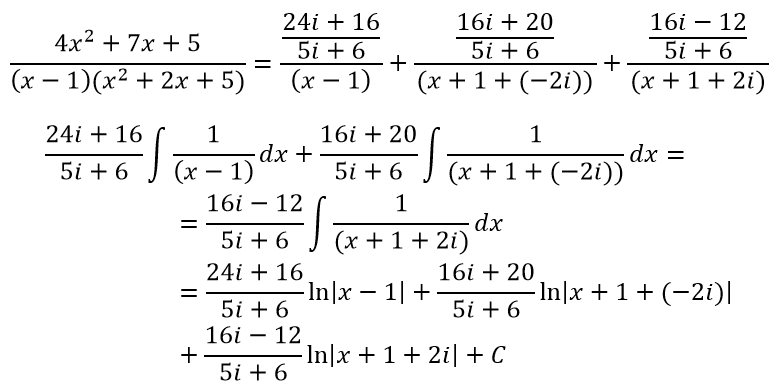Интегрирование рациональных дробей

Допустим дана дробная рациональная функция вида:

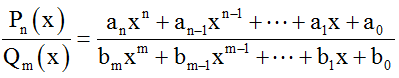
Если m≥n, то данная дробь неправильная.
Если m<n, то данная дробь правильная.

Общий алгоритм интегрирования рациональной дроби:

1. если дробь неправильная, то следует разделить числитель на знаменатель и тем самым исключить целую часть;
2. разложить знаменатель правильной дроби на множители:

P(x)=(x-a)^m,…(x²+px+q)ⁿ

III. Правильную рациональную дробь разложить на простейшие дроби:

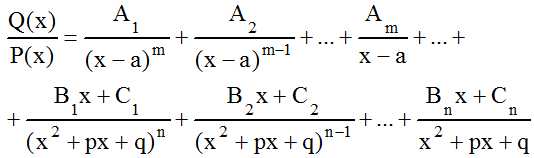
Формулы, применяемые для разложения рациональной дроби:

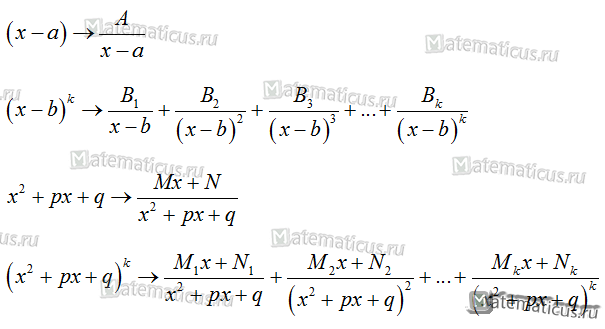
IV. Найти неопределенные коэффициенты A₁, A₂, A_m…B₁,B₂,B_n 

V. Выполнить интегрирование.

Рассмотрим примеры интегрирования рациональных дробей.

---

Пример 1
Найти интеграл:

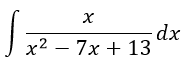
Решение
Исходная дробь правильная.
Разложим знаменатель на множители:

x²-7x+13 = (x-3)(x-4)

Разложение данной дроби имеет вид:

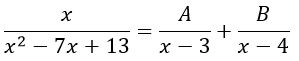
Освобождаясь от знаменателей, получаем:

x = A(x-4) + B(x-3)

x = Ax-4A + Bx-3B

x = (A+B)x-4A-3B

Приравниваем коэффициенты при одинаковых степенях x получаем:

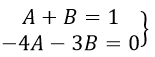
Решив эту систему, находим:

A=-3, B=4

Получаем разложение данной дроби

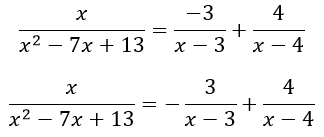
Интегрируя, находим:

---

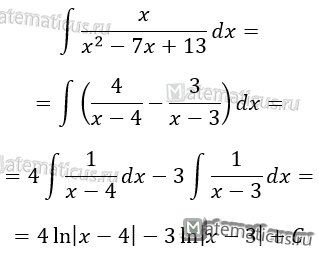
Пример 2
Дана дробь

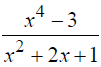
Дробь неправильная, так как числитель больше знаменатель. Необходимо выполнить деление, т.е.

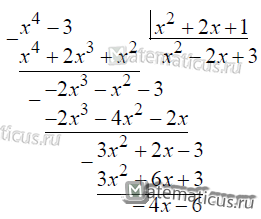
В итоги получаем целую часть и правильную дробь. Интегрирование осуществляем также, как и в примере 1.

---

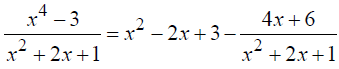
Пример 3
Найти 

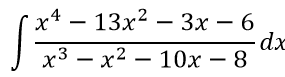
Решение
Выполним преобразование неправильной дроби в правильную (как в примере 2)

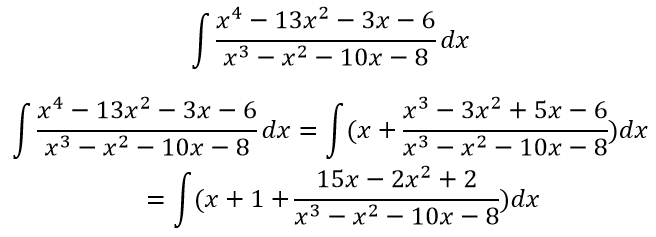
Рассмотрим интеграл:

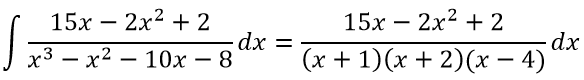
Данная дробь правильная. Разлагаем знаменатель на множители:

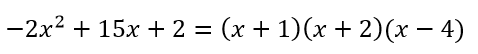
Разложение данной дроби имеет вид:

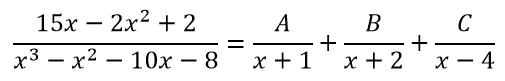
Освобождаясь от знаменателей, получаем:

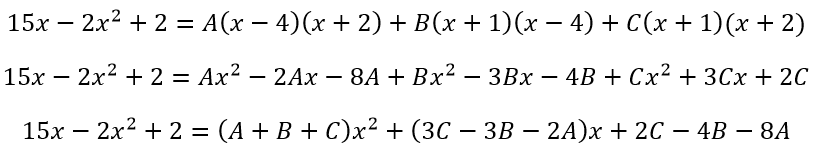
Приравниваем коэффициенты при одинаковых степенях x получаем систему уравнений:

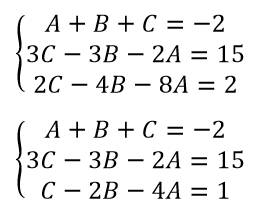
Находим определитель:

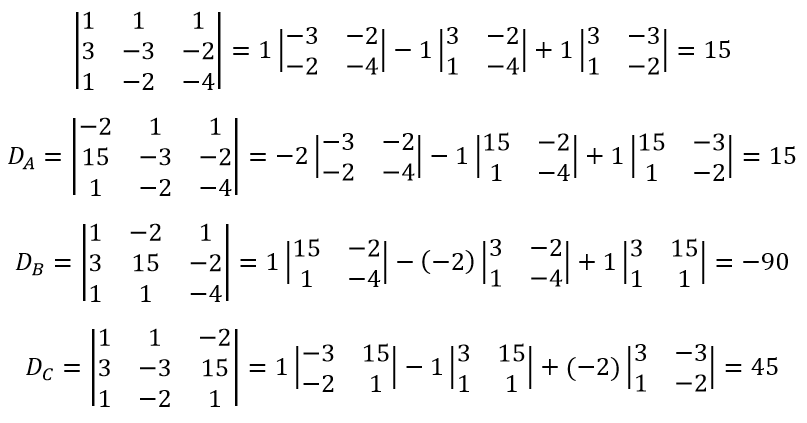
Решив эту систему, находим коэффициенты:

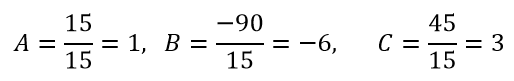
Получаем разложение данной дроби:

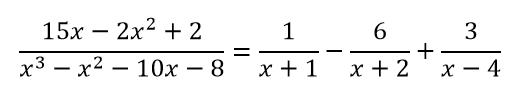
Интеграл примет вид:

---

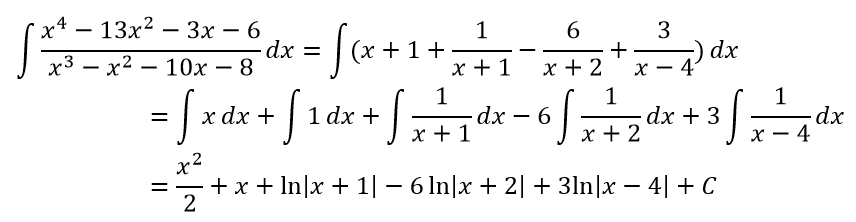
Пример 4
Найти 

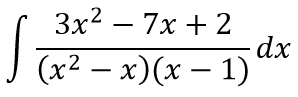
Решение
Выполним преобразования знаменателя

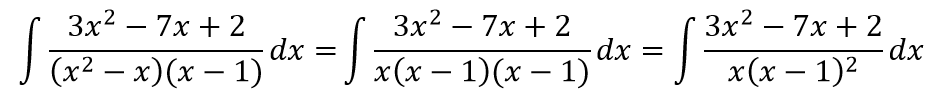
отсюда, множитель x не повторяется, а множитель x-1 повторяется дважды, тогда разложение данной дроби имеет вид:
 
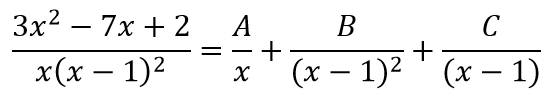
освобождаясь от знаменателей, получаем

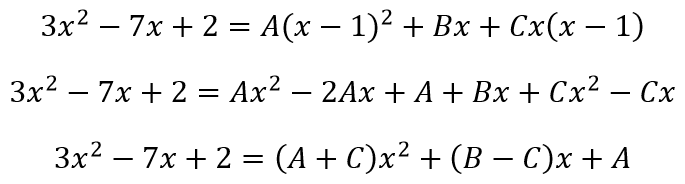
Приравниваем коэффициенты при одинаковых степенях x получаем систему уравнений:

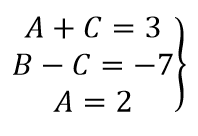
Решив эту систему уравнений, находим коэффициенты:

A=2; B=-2; C=1

В результате получаем разложение данной дроби: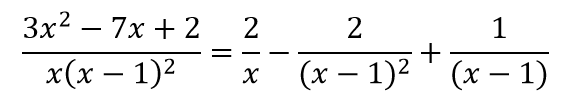
Интегрируя последовательно, находим:

---

Пример 5
Найти 

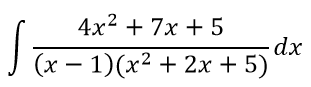
Решение
Преобразуем дробь:

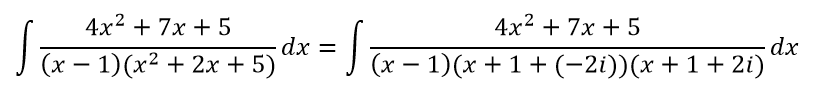
Разложение данной дроби с комплексными числами имеет вид:

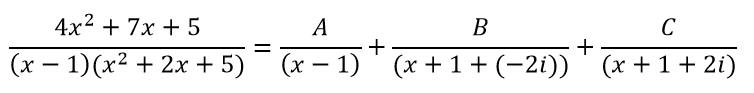
Освобождаясь от знаменателей, получаем:

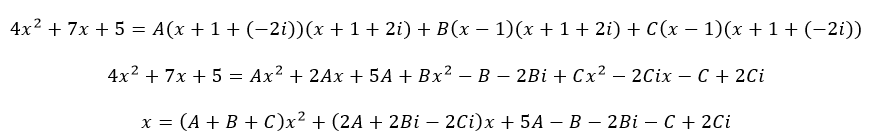
Приравниваем коэффициенты при одинаковых степенях x получаем систему уравнений:

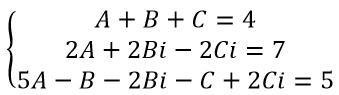
Найдём определитель третьего порядка:

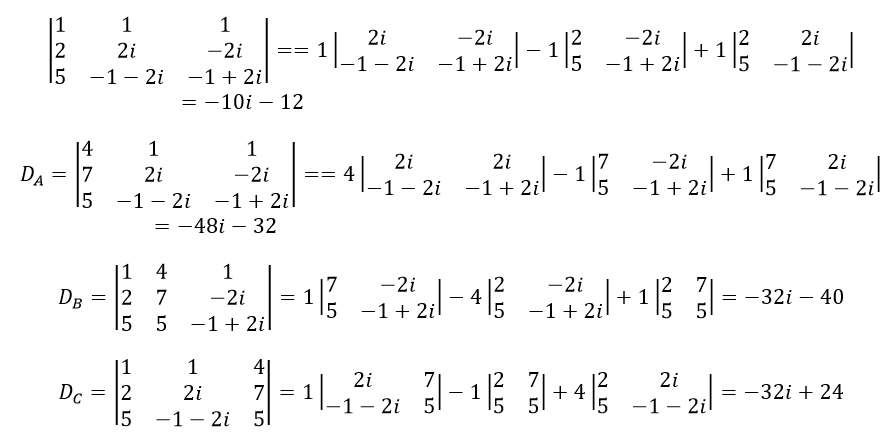
Решив эту систему, находим коэффициенты:

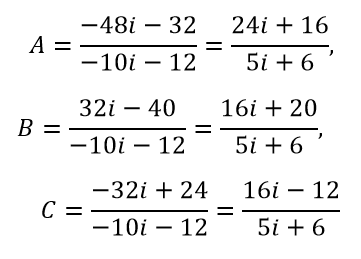
Получаем разложение и решение данной дроби с комплексными числами: