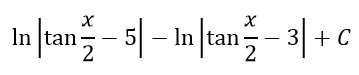Универсальная тригонометрическая подстановка для интегрирования функции

Универсальная тригонометрическая подстановка имеет вид:

$$tg\frac{x}{2} = t$$

К такой подстановки преобразуются в интеграл от рациональной дроби тригонометрические функции sinx, cosx,  по следующем формулам:

---

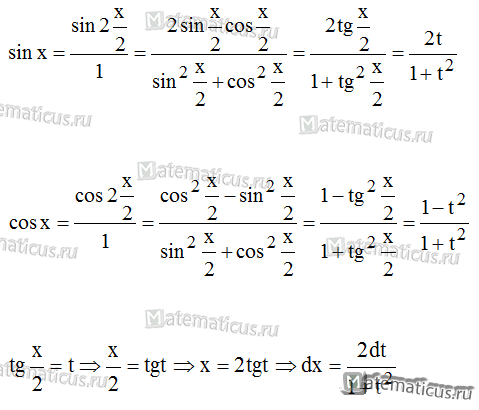
Пример 1
Найти интеграл:
       
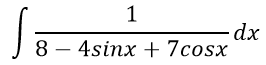
Решение
Интегралы этого вида рационализируются подстановкой $\tan\frac{x}{2}=z$, тогда имеем:

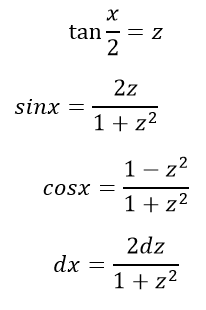
Получаем

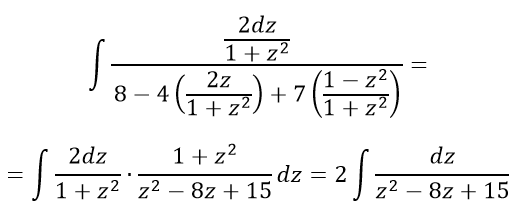
Рассмотрим интеграл

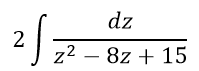
так как дробь правильная, то воспользуемся методом интегрирования рациональных дробей и выполним разложение знаменателя на множители:

$z^2-8z+15=(x-5)(x-3)$

Разложение искомой дроби примет вид:

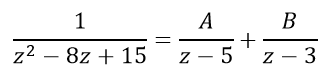
Исключая знаменатель, решаем:

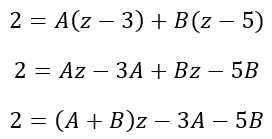
Приравниваем коэффициенты при одинаковых степенях x получаем систему:

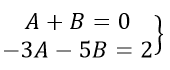
корни системы:

$A=1$, $B=-1$

получаем разложение дроби:

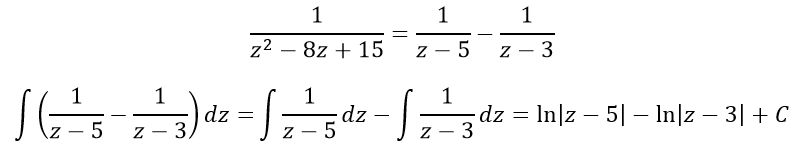
подставляя сюда

$\tan\frac{x}{2}=z$

находим решение интеграла с данной подстановкой