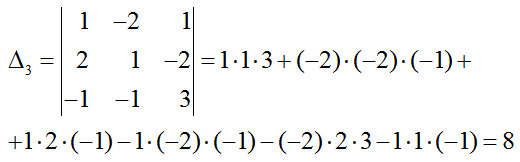Формула определителя третьего порядка выражается зависимостью:
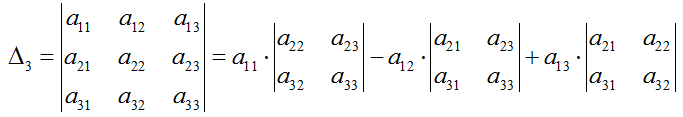
Δ3 — определитель третьего порядка.
Геометрически определитель третьего порядка можно интерпретировать как объем параллелепипеда, построенного на векторах-столбцах матрицы. Если определитель равен нулю, это означает, что вектора линейно зависимы и объем параллелепипеда равен нулю. В случае, когда определитель отличен от нуля, вектора линейно независимы, и объем параллелепипеда ненулевой.
Определитель матрицы обозначается квадратными скобками.
Пример
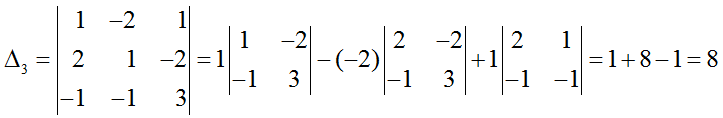
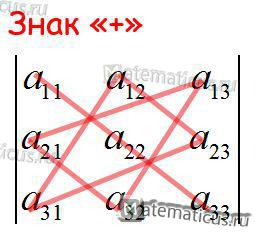
Правило треугольников и правило Саррюса
Также определитель третьего порядка можно найти по правилу треугольников
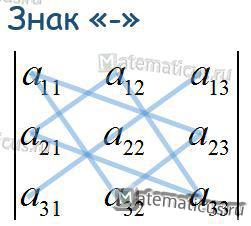
или по правилу Саррюса

И тогда формула для нахождения определителя третьего порядка примет вид:
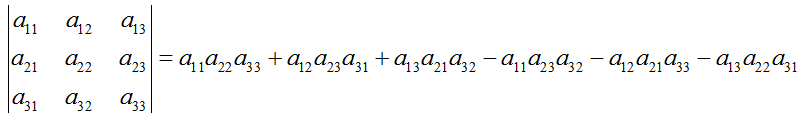
Пример, вычислим значения определителя для той же матрицы, что и выше.