Дифференциальное уравнение вида:
y’ + P(x)y = Q(x) yα
называется уравнением Бернулли.
При α=0 и α=1 уравнение превращается в линейное дифференциальное уравнение первого порядка.
В других случаях решается, опять же к приведению к линейному дифференциальному уравнению 1-ого порядка обе части уравнения разделить на yα и применить метод замены переменной подстановкой z=y1-α или решить с помощью подстановки y=u·v.
По сути уравнением Бернулли тесно связано с линейным уравнением.
Поэтому здесь будет рассмотрен пример с решением.
Пример
Решить уравнение
$$y’ + 2xy = 3{x^3}{y^2}$$
Решение
Обе части уравнения разделим на y2
получаем
$$\frac{{y’}}{{{y^2}}} — 2\frac{x}{y} = 7{x^3}$$
Затем сделаем замену
$$z = \frac{1}{y}$$
отсюда
$$z’ = — \frac{{y’}}{{{y^2}}}$$
Приведём уравнение к линейному ДУ 1-ого порядка
$$z’ + 2xz = — 7{x^3}$$
$$z’ + 2xz = 0$$
$$\frac{{dz}}{z} = — 2xdx$$
$$\ln \left| z \right| = — {x^2} + {C_1}$$
$$z = C{e^{ — {x^2}}}$$
Общее решение уравнения
$$z’ + 2xz = — 7{x^3}$$
найдём в виде
$$z = C(x){e^{ — {x^2}}}$$
тогда
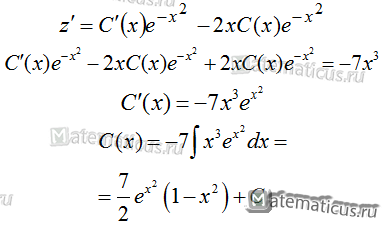
Тогда, общее решение линейного уравнения примет вид
$$z = C{e^{ — {x^2}}} + \frac{7}{2}\left( {1 — {x^2}} \right)$$
Сделаем обратную замену, получим решение данного уравнения
$$y = \frac{2}{{2C{e^{ — {x^2}}} + 7\left( {1 — {x^2}} \right)}}$$
Также решением уравнения является y=0
