Метод вариации произвольной постоянной или метод Лагранжа используется для уравнения вида:
x’ + p(y)x = q(y)
Решением этого уравнения будет математическое выражение:
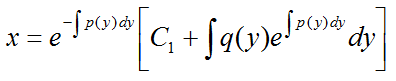
Пример
Решить уравнение
$$\left( {x + {y^2}} \right)dy = ydx$$
Решение
$$\eqalign{& \frac{{\left( {x + {y^2}} \right)dy}}{{ydy}} = \frac{{ydx}}{{ydy}} \cr& \frac{{x + {y^2}}}{y} = \frac{{dx}}{{dy}} \cr& \frac{{dx}}{{dy}} — \frac{1}{y} \cdot x = y \cr} $$
$$\eqalign{& x = {e^{ — \int { — \frac{{dy}}{y}} }} \cdot \left[ {{C_1} + \int {y \cdot {e^{\int { — \frac{{dy}}{y}} }}dy} } \right] = \cr& = {e^{\int {\frac{{dy}}{y}} }} \cdot \left[ {{C_1} + \int {y \cdot {e^{ — \int {\frac{{dy}}{y}} }}dy} } \right] = \cr& = {e^{\ln \left| y \right|}} \cdot \left[ {{C_1} + \int {y \cdot {e^{ — \ln \left| y \right|}}dy} } \right] = \cr} $$
$$\eqalign{ & = y \cdot \left[ {{C_1} + \int {1 \cdot dy} } \right] = \cr & = y \cdot \left( {{C_1} + y} \right) \cr} $$
