Линейные неоднородные ДУ второго порядка с постоянными коэффициентами

Если дифференциальное уравнение имеет вид:

y′′ + py’ + qy = f(x)

то такое уравнение называется линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами и если функция, стоящая в правой части имеет вид

f(x) = P_n(x)e^ax

p, q — коэффициенты;

P_n(x) — многочлен степени n;

a — показатель степени.

Для решения уравнения:

y′′ + py’ + qy = f(x)

которое стоит в левой части, решается как линейное ОДУ второго порядка с постоянными коэффициентами

Решение уравнения стоящего в правой части зависит от решения однородного уравнения стоящего в левой части. Эта зависимость выражается соотношением между корнями k₁, k₂ характеристического уравнения и показателями степени a, перечислим возможные случаи:

---

I. Если a ≠ k₁ ≠ k₂ , тогда частное решение уравнения имеет вид:

y_част = Q_n(x)e^ax

II. Если a ≠ k₁ ≠ k₂ , тогда частное решение уравнения имеет вид:

y_част = x·Q_n(x)e^ax

III. Если a = k₁ = k₂ , тогда частное решение уравнения имеет вид:

y_част = x²·Q_n(x)e^ax

---

В итоги, необходимо найти общее решение однородного уравнения и частное решение уравнения, т.е.

y = y_част + y_общ

---

Пример 1

Решите уравнение

$$y’’- 6y’ + 9y = {e^{3x}}$$

Решение

Общее решение этого уравнения имеет вид:

y = y_част + y_общ

Для однородного дифференциального уравнения 1-ого порядка:

y’’ — 6y’ + 9y = 0

составим характеристическое уравнение:

$$\eqalign{ & {k^2} — 6k + 9 = 0  \cr & {k_{1,2}} = 3 \cr} $$

$${y_{}} = {e^{3x}}\left( {{C_1} + x{C_2}} \right)$$

α=3

Теперь найдем частное решение уравнения

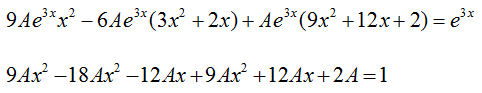
$$2A = 1$$

$$A = \frac{1}{2}$$

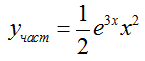
Запишем общее решение уравнения

$$y = {e^{3x}}\left( {{C_1} + x{C_2}} \right) + \frac{1}{2}{e^{3x}}{x^2}$$

---

Пример 2

Решить уравнение

y′′′ — y′ = x² — 1

Решение

Составим характеристическое уравнение, левую часть уравнения приравняем к нулю и найдем корни однородного уравнения с постоянными коэффициентами, получим:

$$\displaylines{ {k^3} — k = 0\quad  \cr k({k^2} — 1) = 0\quad  \cr{k_1} = 0,\quad {k_2} = 1,\quad {k_3} =  — 1 \cr} $$

Найдём общее решение однородного дифференциального уравнения:

$$y = {C_1} + {C_2}{e^x} + {C_3}{e^{ — x}}$$

Частное решение неоднородного уравнения имеет вид:

y_част = x^rQ_n(x)e^ax

Тогда:

$$\displaylines{  Q(x) = A{x^2} + Bx + C \cr   \alpha  = 0,\quad n = 1 \cr} $$

$$y = A{x^3} + B{x^2} + Cx$$

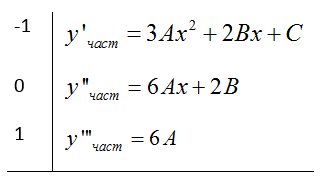
$$6A — 3A{x^2} — 2Bx — C = {x^2} — 1$$

$$\eqalign{&  — 3A = 1  \cr&  — 2B = 0\quad   \cr& 6A — C =  — 1 \cr} $$

$$\displaylines{ A =  — \frac{1}{3} \cr B = 0\quad  \cr C =  — 1 \cr} $$

Получаем решение искомого уравнения:

$$y = {C_1} + {C_2}{e^x} + {C_3}{e^{ — x}} — \frac{1}{3}{x^3} — x$$