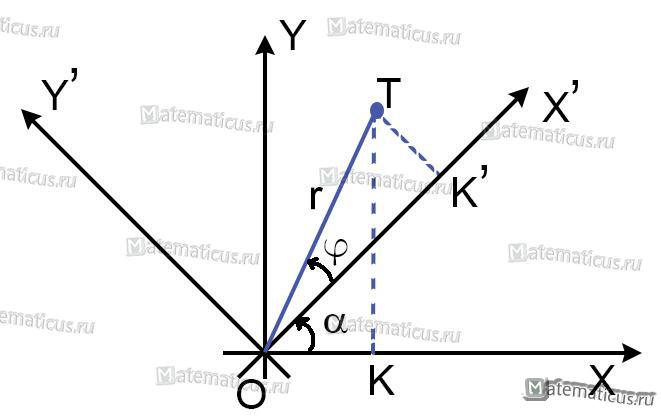
Чтобы найти поворот осей, зададим две системы координат, согласно рисунку
Пусть точка T в новой полярной системе координат имеет полярный радиус r и полярный угол φ. В старой полярной системе координат полярный угол точки T будет равен α+φ, а полярный радиус r будет как в новой системе координат.
Тогда уравнения примут вид:
x = r cos(α+φ)
y = r sin(α+φ)
Применяя тригонометрические тождества суммы двух углов для синуса и косинуса , получим выражения:
x = r (cosα cosφ — sinα sinφ) = r (cosφ) cosα — (r sinφ) sinα
y = r (sinα cosφ + cosα sinφ) = r (cosφ) sinα + (r sinφ) cosα
Обозначим
X = r cosφ и Y = r sinφ
Получим уравнения поворота осей координат
x = X cosα — Y sinα
y = X sinα + Y cosα
Если обозначим следующим образом
x = OK , y = KT — старые координаты точки T
x´= OK´, y´ = KT´ — новые координаты точки T
α — угол поворота осей
тогда формулы поворота осей координат примут вид:

Пример
До поворота осей на угол -300 точка L имела абсциссу x=2 и ординату y=0
Требуется найти координаты точки L после поворота осей.
Решение
Подставляя в формулу, находим новые координаты осей x´, y´
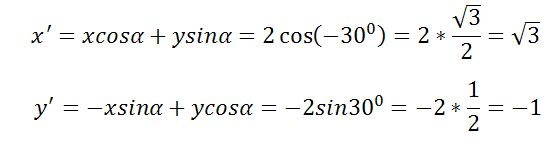

Безобразная ошибка при раскрытии синуса суммы углов. Боюсь, стальные статьи содержат такие же ляпы. Проверяйте! Учите матчасть!
Спасибо вам большое за внимательность, что увидели описку — вместо плюса в формуле минус. Для справки по матчасти, тригонометрические формулы сложения — https://www.matematicus.ru/matematika/trigonometriya/osnovnye-trigonometricheskie-formuly. Извините, но вы тоже написали вместо «стальные» — «остальные» и я вам больше скажу, во всех практически книгах есть тоже описки, вследствие того, что человек не робот, ошибается. И благодаря вашей критики, качество информации повышается)
Какую справочную литературу Вы посоветуете почитать а то я совсем запутался в синусах и косинусах
Можете здесь почитать базовые понятие синуса и косинуса
https://www.matematicus.ru/geometriya/planimetriya/kosinus-sinus-tangens-kotangens
У меня вопрос автору статьи : Какую справочную литературу Вы использовали при написании своей статьи?