Основные тригонометрические формулы

Тригонометрические формулы

sin²α + cos²α = 1

$$tg\alpha = \frac{{\sin \alpha }}{{\cos \alpha }}$$

$$ctg\alpha = \frac{{\cos \alpha }}{{\sin \alpha }}$$

tgα·ctgα = 1

$$t{g^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}$$

$$ct{g^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}$$

---

Формулы сложения

cos(α+b)=cosa·cosb — sina·sinb

cos(α+b)=cosa·cosb + sina·sinb

sin(α+b)=sina·cosb + cosa·sinb

sin(α-b)=sina·cosb — cosa·sinb

$$tg\left( {\alpha + \beta } \right) = \frac{{tg\alpha + tg\beta }}{{1 — tg\alpha \cdot tg\beta }}$$

$$tg\left( {\alpha — \beta } \right) = \frac{{tg\alpha — tg\beta }}{{1 + tg\alpha \cdot tg\beta }}$$

$$ctg(α+β)=\frac{(ctgα\cdot{ctgβ-1})}{ctgα+ctgβ},α,β,α+β≠πn,nϵZ$$
$$ctg(α-β)=\frac{(ctgα\cdot{ctgβ+1})}{(ctgα-ctgβ)},α,β,α-β≠πn,nϵZ$$

---

Формулы суммы и разности

$$\sin \alpha + \sin \beta = 2 \cdot \sin \frac{{\alpha + \beta }}{2} \cdot \cos \frac{{\alpha — \beta }}{2}$$

$$\sin \alpha — \sin \beta = 2 \cdot \sin \frac{{\alpha — \beta }}{2} \cdot \cos \frac{{\alpha + \beta }}{2}$$

$$\cos \alpha + \cos \beta = 2 \cdot \cos \frac{{\alpha + \beta }}{2} \cdot \cos \frac{{\alpha — \beta }}{2}$$

$$\cos \alpha — \cos \beta = — 2 \cdot \sin \frac{{\alpha + \beta }}{2} \cdot \sin \frac{{\alpha — \beta }}{2}$$

$$tg\alpha + tg\beta = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \alpha \cdot \cos \beta }}$$

$$tg\alpha — tg\beta = \frac{{\sin \left( {\alpha — \beta } \right)}}{{\cos \alpha \cdot \cos \beta }}$$

---

Формулы двойного аргумента

sin2α=2·sina·cosa 

cos2α=cos²a+sin²a 

cos2α=1-2sin²a 

cos2α=2cos²a-1 

$$tg2\alpha = \frac{{2tg\alpha }}{{1 — t{g^2}\alpha }}$$

$$ctg2α=\frac{(ctg^2 α-1)}{2ctgα},α≠πn/2,nϵZ$$

---

Формулы половинного аргумента

$${\sin ^2}\frac{\alpha }{2} = \frac{{1 — \cos \alpha }}{2}$$

$${\cos ^2}\frac{\alpha }{2} = \frac{{1 + \cos \alpha }}{2}$$

$$t{g^2}\frac{\alpha }{2} = \frac{{1 — \cos \alpha }}{{1 + \cos \alpha }}$$

$$tg\frac{\alpha }{2} = \frac{{1 — \cos \alpha }}{{\sin \alpha }}$$

$$tg\frac{\alpha }{2} = \frac{{\sin \alpha }}{{1 + \cos \alpha }}$$

$$ctg\frac{α}{2}=\frac{(1+cos⁡α)}{sin⁡α}=\frac{sin⁡α}{(1-cos⁡α)},α≠πn,nϵZ$$

---

Формулы тройного угла

sin3α=3sinα — 4sin³a

cos3α=4cos³α — 3cosa

$$tg3α=\frac{(3tgα-tg^3α)}{(1-3tg^2α)},α≠\frac{π}{6}(2n+1),nϵZ$$
$$ctg3α=\frac{(3ctgα-ctg^3α)}{(1-3ctg^2α)},α≠\frac{πn}{3},nϵZ$$

---

Формулы понижения степени

$${\sin ^2}\alpha = \frac{{1 — \cos 2\alpha }}{2}$$

$${\cos ^2}\alpha = \frac{{1 + \cos 2\alpha }}{2}$$

---

Формулы произведения

$$\sin \alpha \cdot \sin \beta = \frac{1}{2}\left( {\cos \left( {\alpha — \beta } \right) — \cos \left( {\alpha + \beta } \right)} \right)$$

$$\sin \alpha \cdot \cos \beta = \frac{1}{2}\left( {\sin \left( {\alpha — \beta } \right) + \sin \left( {\alpha + \beta } \right)} \right)$$

$$\cos \alpha \cdot \cos \beta = \frac{1}{2}\left( {\cos \left( {\alpha — \beta } \right) + \cos \left( {\alpha + \beta } \right)} \right)$$

---

Дополнительные формулы

$$\sin \alpha + \cos \alpha = \sqrt 2 \cdot \sin \left( {x + \frac{\pi }{4}} \right)$$

$$\sin \alpha — \cos \alpha = \sqrt 2 \cdot \sin \left( {x — \frac{\pi }{4}} \right)$$

---

Формулы преобразования суммы и разности тригонометрических функций в произведение

 

---

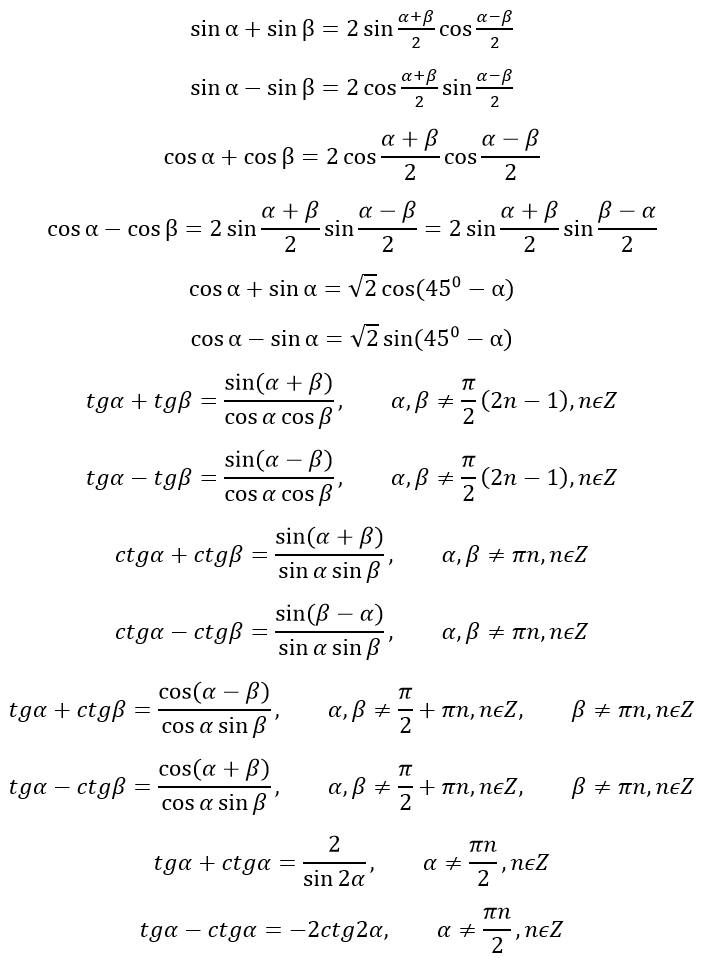
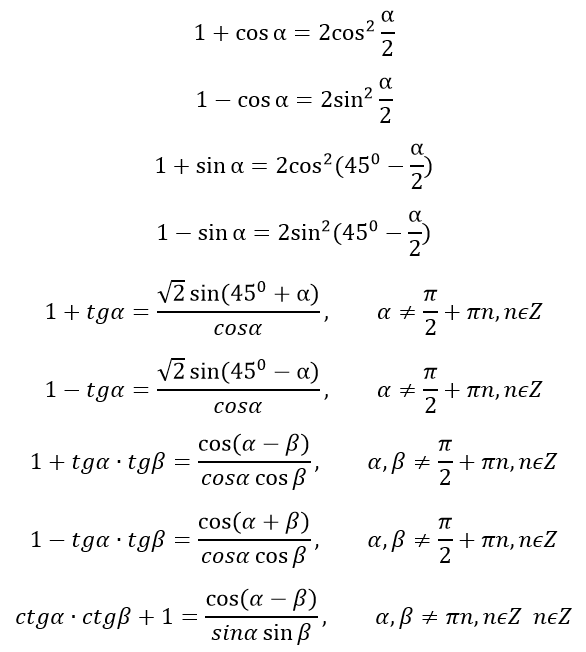
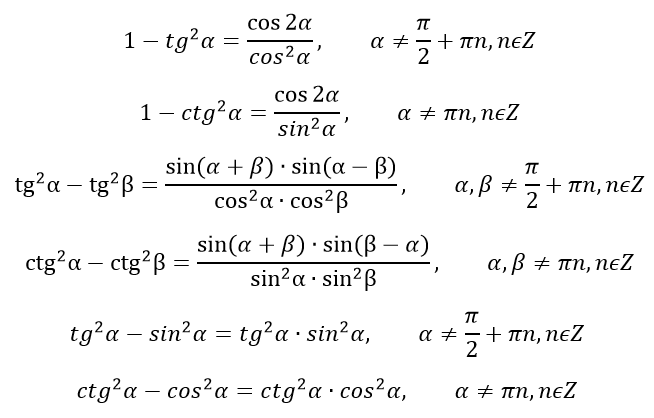
Формулы преобразования произведения тригонометрических функций

---

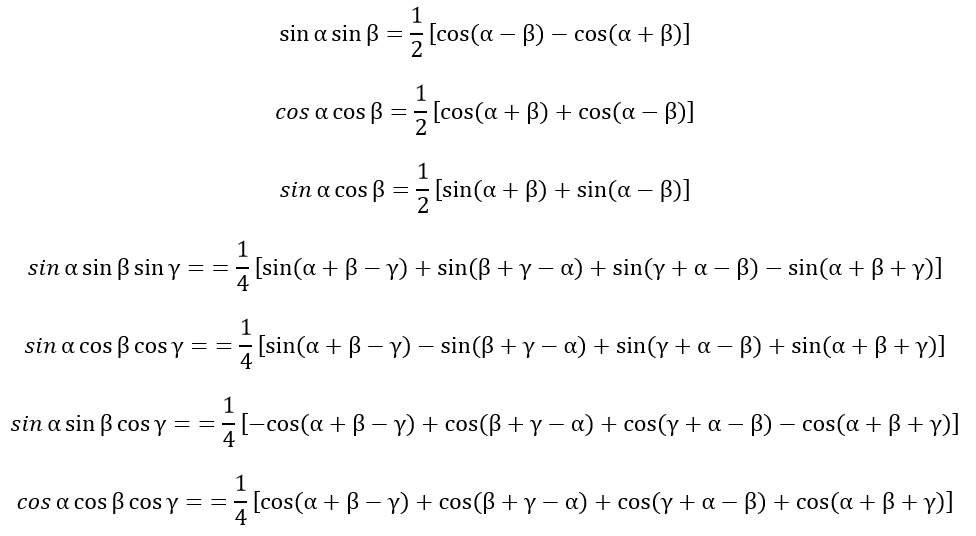
Формулы, выражающие тригонометрические функции через тангенс половинного аргумента

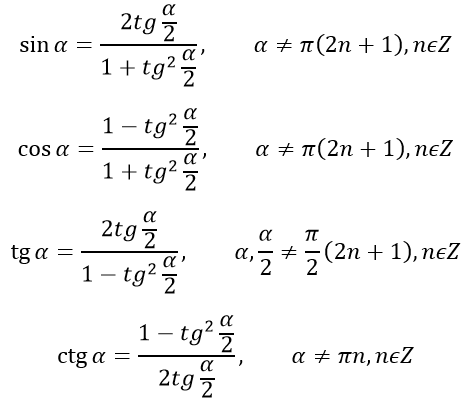
Скачать шпаргалку по основным тригонометрическим формулам