Гистограмма представляет собой ступенчатую фигуру в виде прямоугольников. Длина каждого прямоугольника представляет собой равный одинаковый частотный интервал и вычисляется по формуле:
xi-xi-1
Высоты гистограммы определяется по формуле:
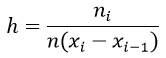
Формула размаха выборки R:
R=xmax−xmin
Количество интервалов в выборке определяется по формуле:
k≈1+log2n≈1+3,221·lgn
Длина l интервала гистограммы, формула:
l=R/n
Формула эмпирической плотности распределения выборки имеет вид:
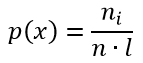
хi — значения частот;
ni — частоты;
wi — относительные частоты;
n — объём выборки;
Пример
В водоёме проведены измерения температуры воды в течение 20 дней.
Статистика отчета измерений:
11, 15, 18, 14, 12, 13, 11, 14, 18, 19, 18, 14, 15, 16, 14, 18, 21, 17, 13, 16
Построить гистограмму относительных, абсолютных и накопленных частот выборки, вычислить эмпирическую плотность распределения частот.
Решение.
По условию задачи объем выборки равен 20.
Отсортируем и упорядочим вариационный ряд, начиная от самого минимального значения, получим:
11, 11, 12, 13, 13, 14, 14, 14, 14, 15, 15, 16, 16, 17, 18, 18, 18, 18, 19, 21
Найдем размах выборки
R=21-11=10
Количество интервалов в выборке равно:
k≈log220+1≈5,32
Округляя до целого числа, имеем
k=5
Определим длину каждого интервала
l=10/5=2
Получаем таблицу интервалов
| Номер интервала | Абсолютная частота, ni | Частотный интервал |
| 1. | 3 | [11;13) |
| 2. | 6 | [13;15) |
| 3. | 4 | [15;17) |
| 4. | 5 | [17;19) |
| 5. | 2 | [19;21) |
Таблица относительных частот и эмпирическая плотность распределения частоты
| Частотный интервал | Относительная частота, wi=ni/n | Эмпирическая плотность распределения частоты ni/Δ |
| [11;13) | 0.15 | 1.5 |
| [13;15) | 0.3 | 3 |
| [15;17) | 0.2 | 2 |
| [17;19) | 0.25 | 0.25 |
| [19;21) | 0.1 | 0.1 |
График гистограммы абсолютных частот
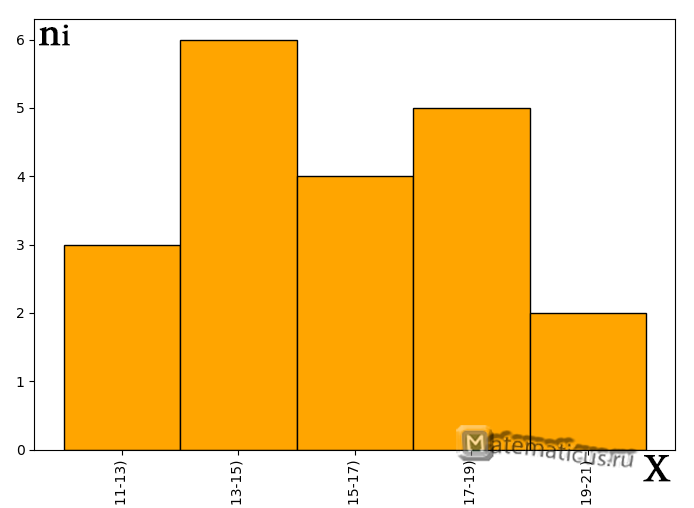
График гистограммы относительных частот
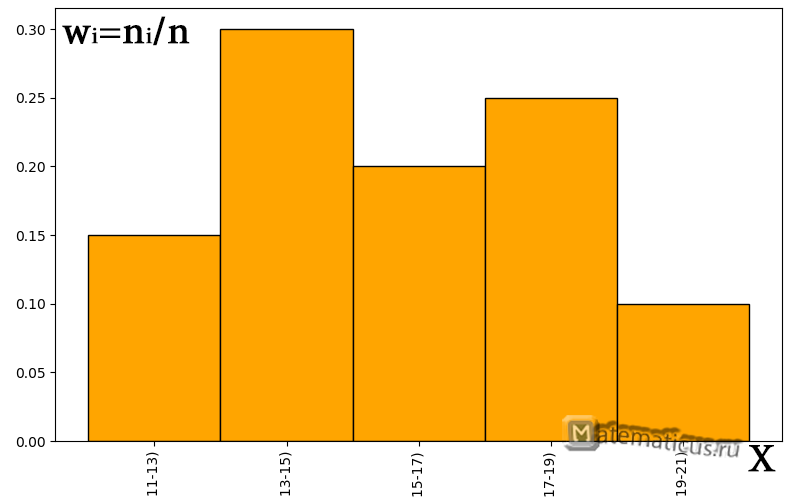
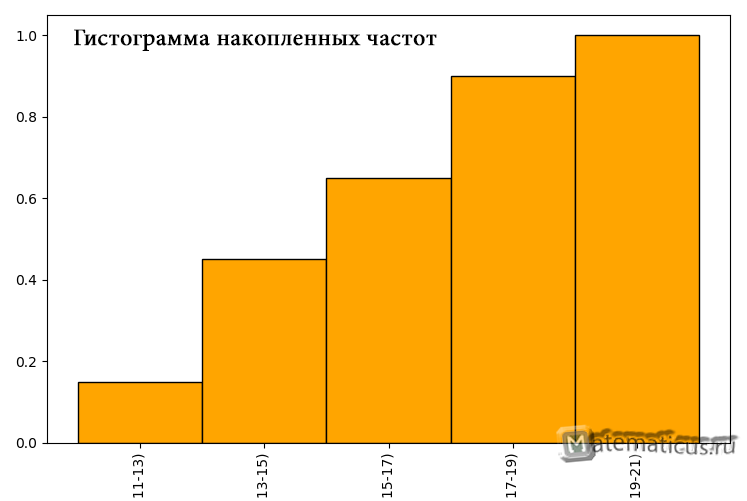
График гистограммы накопленных частот
Полигон это тоже самое, что и многоугольник распределения вероятностей или частот и строится для дискретной случайной величины.
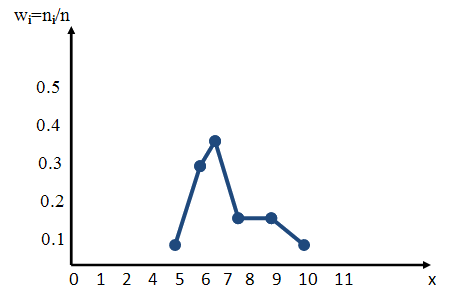
Полигон в статистике — это график (или ломанная линия), отрезки которой соединяют точки с координатами хi, wi в прямоугольной системе координат между собой (см. рисунок ниже) и наглядно показывает распределение частот как для количественных, так и порядковых значений переменных, то плотность распределения случайной величины.
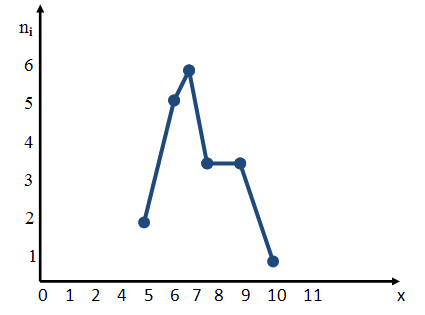
Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им частоты ni и соединяют точки.
Пример графика полигона частот хi, ni
Пример графика полигона относительных частот хi, wi