Плотность распределения вероятностей (плотность распределения) случайной величины — первая производная от функции распределения.
Другими словами, плотность вероятности — это некоторая средняя вероятность, приходящая на бесконечно малый отрезок.
Функция распределения — это первообразная плотности распределения вероятностей.
Обозначение плотности вероятности распределения: p(x) или f(x)
Обозначение функции распределения: F(x)
Вероятность попадания случайной непрерывной величины X в промежуток (а, b) можно вычислить с помощью плотности распределения вероятностей р(х), которая является производной от функции распределения F(x), т.е.
F'(х) = р(х)
Поэтому
P(a≤x<b) = $\mathop \smallint \limits_b^a $p(x)dx = F(b) − F(a)
Замечание
Плотность вероятностей неотрицательная функция:p(x) > 0
Пример
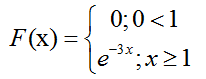
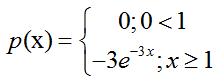
Найдем вероятность случайной величины X в промежутке (-2; 3)
Запишем выражение из условия
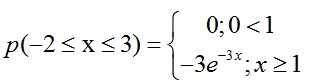
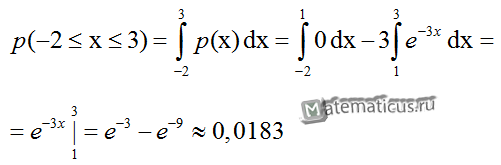
Выражение e–5 эквивалентно выражению 1/e5
