Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х1, х2,…,хn этой величины и их вероятностями p1, p2,…,pn
Может быть задан аналитически, графически или таблично.
Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть
| X | x1 | x2 | …… | xn |
| P | p1 | p2 | …… | pn |
х1, х2,…,хn — значения дискретной случайной величины;
p1, p2,…,pn — вероятности значений X дискретной случайной величина.
Также должно выполняться условия, что сумма вероятностей равна 1, то есть
∑p=p1+p2+ … +pn=1
Графически закон распределения ДСВ задается в виде многоугольника распределения см. здесь., а аналитически, например, с применением формулы Бернулли.Рассмотрим примеры
Пример 1
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение
Вероятности равны:
p1(6)=6/10=0,6;
p2(4)=4/10=0,4
| X | 6 | 4 |
| P | 0.6 | 0.4 |
Пример 2
Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение
Объем выборки равен
n=4+6+8+2=20
X принимает следующие значения:
x1=4; x2=6; x3=8; x1=2
Найдем их вероятности:
p1(4)=4/20=0,2;
p2(6)=6/20=0,3;
p3(8)=8/20=0,4;
p4(2)=2/20=0,1
Получаем таблицу закона распределения дискретной случайной величины
| X | 4 | 6 | 8 | 2 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение
n=5+13+7=26
Вычислим вероятности:
Таблица имеет вид:
| X | 5 | 13 | 8 | 2 |
| P | 0.2 | 0.52 | 0.28 | 0.1 |
Пример 4
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем:
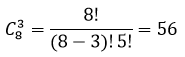
при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при P(X=2) — вероятность того, что среди трех отобранных изделий окажется два стандартных и одно нестандартное изделие;
при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные.
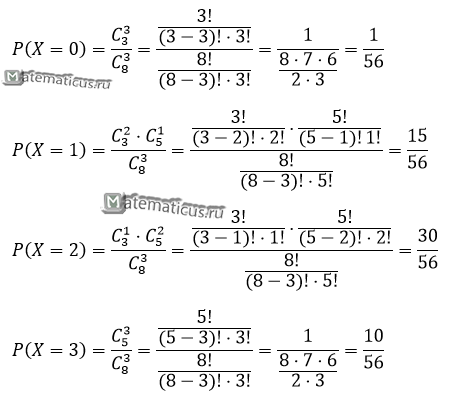
Составим таблицу распределения
| X | 0 | 1 | 2 | 3 |
| P | 0.018 | 0.268 | 0.536 | 0.178 |
Пример 5
В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных.
Решение
Возможные варианты значений СВ X: 1, 2, 3
$n=C_6^3$ — числу способов, которыми можно выбрать три детали из шести;
$C_4^x$ — число способов, которыми из четырех деталей выбирают х деталей.
$C_2^{3 — x}$ — общее число способов отбора нестандартных деталей
Тогда вероятности события A вычисляются по формуле
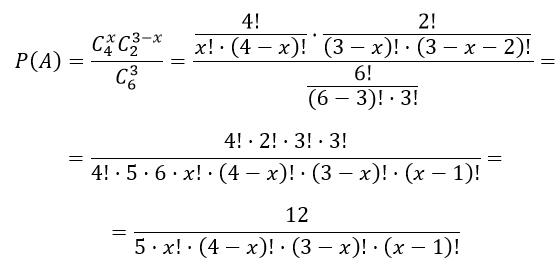
Закон распределения дискретной случайной величины X для составления ряда распределения:
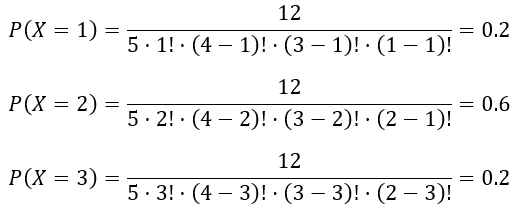
Получаем таблицу ряда распределения ДСВ
| X | 0 | 1 | 2 | 3 |
| P | 0 | 0.2 | 0.6 | 0.2 |
