Дискретная случайная величина X имеет геометрическое распределение, если ее закон распределения имеет следующий вид:
Pm=pqm-1
где
q=1-p
Математическое ожидание вычисляется по формуле:
$M(X) = \frac{1}{p}$
Формула дисперсии имеет вид:
$D(X) = \frac{q}{{{p^2}}}$
Пример
В отдел информационных технологий поступило 16 мониторов. По статистическим данным 1 из 16 мониторов неисправен, следовательно, 1/16=0,0625 — вероятность того, что монитор неисправен. Отделом проводится проверка всех мониторов. Требуется составить закон распределения проверки мониторов и обнаружения неисправных.
Решение
Составим вспомогательную таблицу
| m | p | qm-1 | Pm |
| 1 | 0,0625 | 1 | 0,0625 |
| 2 | 0,0625 | 0,9375 | 0,058594 |
| 3 | 0,0625 | 0,878906 | 0,054932 |
| 4 | 0,0625 | 0,823975 | 0,051498 |
| 5 | 0,0625 | 0,772476 | 0,04828 |
| 6 | 0,0625 | 0,724196 | 0,045262 |
| 7 | 0,0625 | 0,678934 | 0,042433 |
| 8 | 0,0625 | 0,636501 | 0,039781 |
| 9 | 0,0625 | 0,596719 | 0,037295 |
| 10 | 0,0625 | 0,559425 | 0,034964 |
| 11 | 0,0625 | 0,52446 | 0,032779 |
| 12 | 0,0625 | 0,491682 | 0,03073 |
| 13 | 0,0625 | 0,460952 | 0,028809 |
| 14 | 0,0625 | 0,432142 | 0,027009 |
| 15 | 0,0625 | 0,405133 | 0,025321 |
| 16 | 0,0625 | 0,379812 | 0,023738 |
| «17» | 0,356074 | 0,356074 |
Построим полигон распределения СВ.
В таблице m=17 — проверяемые мониторы все исправны и составляет P17≈0,36.
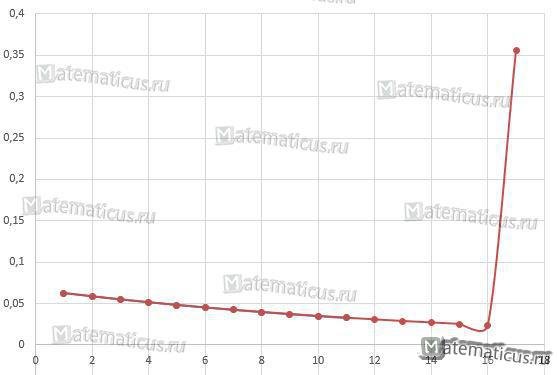
Из графика видно, что чем больше m, тем вероятность обнаружения неисправного монитора снижается.
