Эмпирической (опытной) функцией распределения или функцией распределения выборки называют такую функцию, которая определяет для каждого значения x частоту событий X<x и предназначена для оценке теоретической функции распределения генеральной совокупности в математической статистике.
Эмпирическая функция распределения находится по формуле:
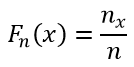
n — объем выборки;
nx — количество наблюдений (вариантов) меньше x.
Пример
Дана таблица функции распределения выборки. Требуется построить эмпирическую функцию распределения
| xi | 1 | 2 | 3 | 4 | 5 | 6 |
| ni | 4 | 10 | 6 | 8 | 7 | 5 |
Решение
Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки
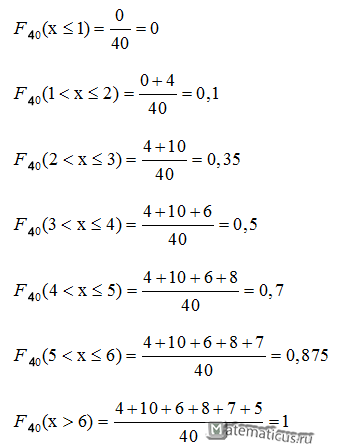
Эмпирическая функция распределения имеет вид

Построим график кусочно-постоянной эмпирической функции распределения
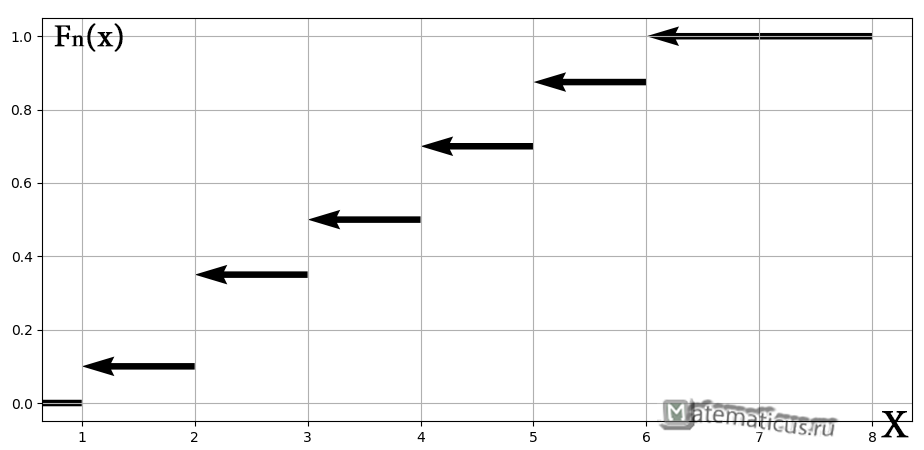
таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.

У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.
Исправили. Спасибо Вам большое за внимательность)
Не понял физического смысла эмпирического распределения — что она нам дает?
Определяет для каждого значения частоту события