Пусть совокупность событий H1,H2,…,Hn — образуют полную группу событий, а также их объединение даёт достоверное событие и они попарно несовместные. В случае наступления каждого из событий Hi, событие А может настать с некоторой условной вероятностью PHi·(A)
События Hi называют гипотезами.
Запишем формулу полной вероятности:
P(A)=P(H1)·PH1(A)+P(H2)·PH2(A)+…+P(Hn)
или эту формулу можно представить в следующем виде:
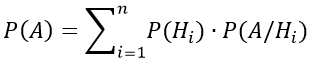
Пример 1
В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
Решение
А — «мишень поражена»
H1 : «выстрел из винтовки с оптическим прицелом»
H2 : «выстрел из винтовки без оптического прицела»
Находим вероятности
Р(H1)=3/5=0.6, Р(H2) =2/5=0.4
РH1(А)=0.95, РH2(А)=0.7
Итак, по формуле полной вероятности находим вероятность
Р(А)=P(H1)·PH1(A)+P(H2)·PH2(A)=0,57·0,92+0,43·0,8=0,524+0,344=0,868
Пример 2
В вычислительной лаборатории имеются шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
Решение
А — «до конца расчета машина не выйдет из строя»
H1 — «клавишный автомат не выйдет из строя»
H2 — «полуавтомат не выйдет из строя»
Из условия задачи получаем
Р(H1)=6/10=0,6 Р(H2)=4/10=0,4
Условные вероятности равны
РH1(А)=0.95, РH2(А)=0.8
Воспользуемся формулу полной вероятности, имеем:
Р(А)=P(H1)·PH1(A)+P(H2)·PH2(A)=
=0,6·0,95+0,4·0,8=0,89
Пример 3
Экзамен сдают студенты трех групп. В первой группе 7, во второй 6 и в третьей 8 студентов. Студент из первой группы сдаст экзамен с вероятностью 0.9, из второй группы с вероятностью 0.8 и из третьей группы с вероятностью 0.7. С какой вероятностью сдаст экзамен случайно вызванный студент?
Решение
Cобитые А — «случайно вызванный студент сдаст экзамен»
Н1: студент из 1-ой группы
Р(H1)=7/21; Р(A|H1)=0.9
Н2: студент из 2-ой группы
Р(H2)=6/21; Р(A|H2)=0.8
Н3: студент из 3-ей группы
Р(H3)=8/21; Р(A|H3)=0.7
По формуле полной вероятности получаем:
Р(А)=P(H1)·Р(A|H1)+P(H2)·Р(A|H2)+P(H3)·P(A|H3)=
=7/21·0.9+6/21·0.8+8/21·0.7=0.795
Пример 4
В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
Решение
A— «наудачу извлечённый из двух выбранных шаров — белый шар»
H1: «шар извлечен из первой урны»
H2: «шар извлечен из второй урны»
По условию задачи, следует, что из каждой урны извлекается одинаковое количество шаров, тогда получаем вероятности
Р(H1)=Р(H2)=1/2
Найдем условные вероятности того, что из первой урны
РH1(A)=8/10=3/10
и второй урны извлечен белый шар
РH2(A)=4/20=1/5
Применяя формулу полной вероятности, найдем вероятность того, что взят белый шар
Р(А)=P(H1)·PH1(A)+P(H2)·PH2(A)=
=1/2·4/5+1/2·1/5=1/2
