Формула Байеса имеет вид:
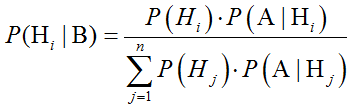
Здесь событие А может произойти в случае появлении одного из несовместных событий Н1, Н2, Н3,…,Нn.
H — гипотеза.
Рассмотрим применение формулы Байеса при решении типовых задач.
Пример 1
В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
Решение
А — «стрелок поразил мишень».
H1 — «мишень поражена из оптической винтовки»
H2 — «мишень поражена из винтовки без оптического прицела»
Р(H1)=4/10=0.4, Р(H2)=6/10=0.6
Условные вероятности из условия задачи равны
Р(H1|А)=0.95, Р(H2|А)=0.8
Применим формулу полной вероятности и найдём вероятность события А:
Р(А)=Р(H1)·Р(H1|А)+Р(H2)·Р(H2|А)=
=0.4·0.95+0.6·0.8=0,86
Воспользуемся формулой Байеса, найдем вероятности РА(H1) и РА(H2):
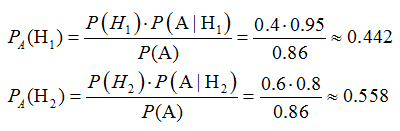
Из решения следует, что
РА(H1)<РА(H2)
значит вероятнее всего, что стрелок стрелял из винтовки без оптического прицела.
Пример 2
Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму — 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым — 0,98. стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.
Решение
А — «изделие при проверке было признано не бракованным»
Н1— «изделие попало к первому товароведу»
Н2 — «изделие попало ко второму товароведу»
Р(H2)=0.55, Р(H1)=0.45
Условные вероятности того, что изделия признаны стандартным первым и вторым товароведами равны
Р(H1|А)=0.9, Р(H2|А)=0.98
Применим формулу Байеса, чтобы найти вероятность того, что это изделие проверил второй товаровед:
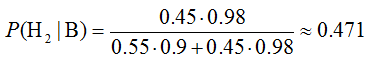
Пример 3
Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.
Решение
А — «два стрелка поразили мишень»
H1 — «третий стрелок поразил мишень»
H2 — «третий стрелок промахнулся»
Р(H1)=0.4, Р(H2)=1-Р(H1)=1-0.4=0.6
Найдем условную вероятность Р(H1|А) того, что мишень будет поражена первым или вторым орудиями и при этом третье орудие попала в цель.
Р(H1|А)=p1·q2+q1·p2
р1 — вероятность попадания первым стрелком;
р2 — вероятность попадания вторым стрелком;
q1 — вероятность промаха первым стрелком;
q2 — вероятность промаха вторым стрелком.
Р(H1|А)=0.6·(1-0.5)+(1-0.6)·0.5=0.3+0.2=0.5
Условная вероятность того, что цель будет поражена первым и вторым стрелком, при условии, что третье орудие не поразило цель. Так как события независимые, применяем теорему умножения, получаем:
Р(H2|А)=p1·p2=0.6·0.5=0,42
По формуле Байеса, получаем
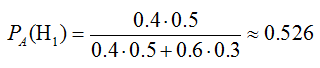
Пример 4
На трех дочерей: Машу, Дашу и Наташу в семье возложена обязанность мыть посуду. Поскольку Маша старшая ей приходится выполнять 40 % работы. Остальные 60 % делят между собой Даша и Наташа. Когда Маша моет посуду, вероятность разбить равна 0,02, для Даши — 0,02, для Наташи — 0,03. Родители не знают, кто вечером мыл посуду, но слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла а) Маша, б) Даша, в) Наташа.
Решение
Событие А – тарелка разбита.
Н1 – мыла Маша;
Н2 – мыла Даша;
Н3 – мыла Наташа.
Р(Н1)=0,4; Р(Н2)=0,3; Р(Н3)=0,3
Из условия задачи Р(H1|А)=0,02, Р(H2|А)=0,02, Р(H2|А)=0,03
Таким образом, пользуясь формулой Байеса, получаем решения для каждого случая:

