Если в n испытаниях событие А случается (происходит) k раз и не случается (не происходит) (n-k) раз, то данную вероятность Рn(k) можно найти по формуле Бернулли:
![]()
где
p — вероятность успеха испытания (опыта);
q=1-p — вероятность неудачи испытания (вероятность противоположного события);
$C_n^k$ — число сочетаний, вычисляется по формуле комбинаторики — сочетание без повторения
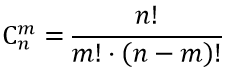
Пример 1
Монету бросают шесть раз. Найти вероятность того, что герб выпадет не менее двух раз.
По условию, n=6, k=2
Вероятность выпадения орла и герба одинаковая, значит p=1/2=0.5, a q=1-p=0.5
применим формулу Бернулли
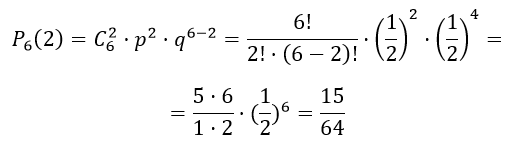
Пример 2
Каждый день акции компании X поднимаются в цене или падают в цене на один пункт с вероятностями 0,75 и 0,25. Найти вероятность того, что акции после 6 дней вернутся к своей первоначальной цене, то есть чтобы акции за это время 3 раза поднялись в цене и три раза опустились в цене. При этом изменения цены акции вверх и вниз – независимые события.
Решение
${P_6}\left( 3 \right) = C_6^3{\left( {\frac{3}{4}} \right)^3}{\left( {\frac{1}{4}} \right)^3} = 0,13$
Пример 3
По каналу связи передаётся 10 сообщений, каждое из которых независимо от других с вероятностью р = 0,2 искажается помехами. Найти вероятность того, что:
a) из 10 сообщений ровно 3 будет искажено помехами;
б) все сообщения будут приняты без искажений;
в) не менее двух сообщений будет искажено.
Решение
a)
Вероятность искажения равна $р ={\frac{1}{5}}$
, а не неискажения $q=1–p={\frac{4}{5}}$
n = 10, k = 3
Тогда вероятность того, что из 10 сообщений ровно 3 будет искажено помехами равна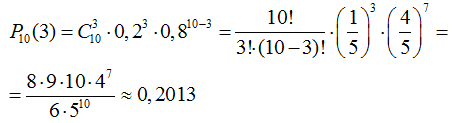
б)
Тогда вероятность того, что все сообщения будут приняты без искажений равна
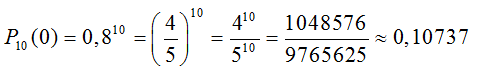
в)
Тогда вероятность того, что не менее двух сообщений будет искажено равна
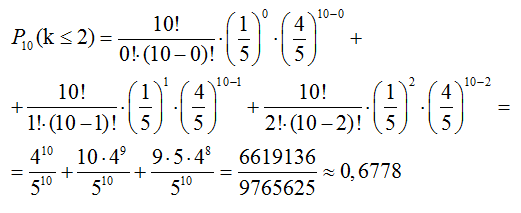
Пример 4
Два равносильных противника играют в шахматы.
Что вероятнее:
а) выиграть одну партию из двух или две партии из четырех?
б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.
Решение
Вероятность выигрыша шахматиста равна р=1/2, а вероятность проигрыша шахматиста
q=1-p=0.5
а) По формуле Бернулли найдём вероятность P2(1) «выиграть одну партию из двух» и вероятность P4(2) «выиграть две партии из четырех»
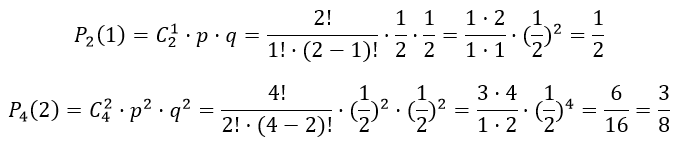
Имеем P2(1)>Р4(2) следовательно, вероятнее в шахматы выиграть одну партию из двух, чем две партии из четырех.
б) Сначала рассмотрим событие A — «выиграть не менее двух партий из четырех», которое соответствует сумме независимых событий Р4(2), Р4(3), Р4(3), то есть «выиграть две или три или четыре партии из четырех»
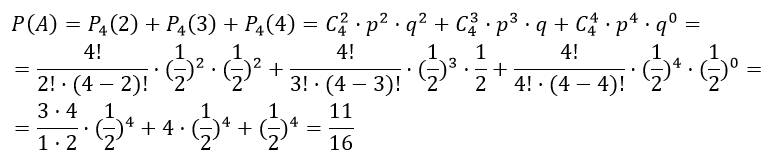
Теперь рассмотрим событие В — «выигрыш не менее трех партий из пяти», которое соответствует сумме независимых событий Р5(3), Р5(4), Р5(5), то есть «выиграть три или четыре или пять партий из трех»
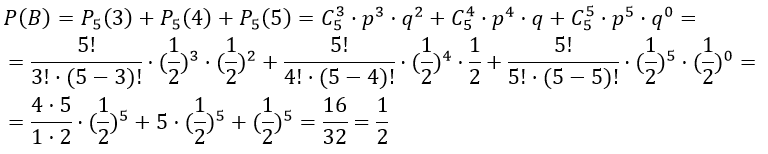
Здесь Р(А)>P(B), следовательно, вероятнее выиграть не менее двух партий из четырех, чем не менее трех партий из пяти.
