Критерий Фишера

Критерий Фишера используют в качестве проверке равенства (однородности) дисперсий двух выборок, в том числе проверки значимости модели регрессии.

 Критерий Фишера находится по формуле:

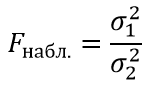
при σ₁>σ₂

σ₁ – большая дисперсия выборки;

σ₂ – меньшая дисперсия выборки.

Формула критерий Фишера для оценки значимости уравнения регрессии:

 

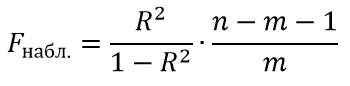
При F_набл<F_кр нулевая гипотеза принимается.

Число степеней свободы исправленных дисперсий находятся по формулам:

для первой выборки

f₁=n₁−1

для второй выборки

f₂=n₂−1

 F_кр (α, f₁, f₂) определяется по таблице

---

Пример
Дана выборка успеваемости по двум группам.

№ п/п	X	Y
1	34	45
2	44	68
3	97	76
4	62	56
5	39	78
6	73	64
7	42	84
8	95	54
9	35	81
10	37	79
11	45	41
12	43	47
13	73	79
14	53	32
15	32	44

Требуется определить различия в оценках между двумя группами при α = 0.05.
Решение
Вычислим дисперсию по X и по Y

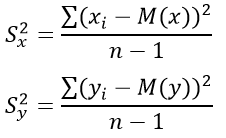
№ п/п	X	Y	D(X)	D(Y)
1	34	45	27,44	20,32
2	44	68	6,5829	2,687
3	97	76	134,54	14,268
4	62	56	5,04	2,4584
5	39	78	15,226	18,592
6	73	64	26,883	0,3251
7	42	84	9,6114	34,992
8	95	54	122,43	4,4203
9	35	81	24,711	26,149
10	37	79	19,683	20,968
11	45	41	5,2829	31,101
12	43	47	8,0257	15,787
13	73	79	26,883	20,968
14	53	32	0,0257	63,716
15	32	44	33,326	22,801
Сумма	804	928	465,69	299,55
Среднее	53,6	61,867

Пример вычисления D(X1) и D(Y1):

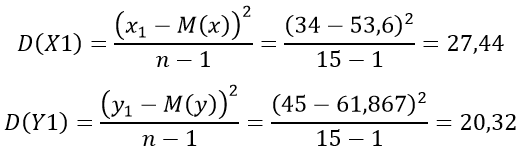
и т.д.

Смотрите результаты вычислений в таблице выше. Отсюда находим значения S²_x и S²_y  по первой и второй выборкам:

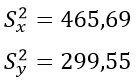
По критерию Фишера находим F_эмп.

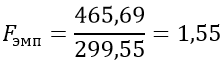
k₁=15 — 1 = 14 (количество значения признака в первой выборке),
k₂=15 — 1 = 14 (количество значения признака во второй выборке)
По таблице критерия Фишера находим критическое значение
F_крит=2.49, следовательно, 2.49>1.55, F_крит>F_эмп

Отсюда, различия в оценках между двумя выборками групп присутствует, принимаем гипотезу.