Степенной ряд —  это функциональный ряд вида:

$$\sum\limits_{n = 0}^\infty  {{u_n}(x)}  = \sum\limits_{n = 0}^\infty  {{a_n} \cdot {{(x — a)}^n}}  = {a_0} + {a_1}(x — a) + … + {a_n}{(x — a)^n} + …$$

a_n— коэффициент ряда.

Если a=0, то ряд принимает вид:

$$\sum\limits_{n = 0}^\infty {{a_n} \cdot {x^n}} = {a_0} + {a_1}x + {a_2}{x^2} + … + {a_n}{x^n} + …$$

---

Теорема Абеля

Если данный степенной ряд сходится при x=x₀≠0, то он абсолютно сходится при ∀x  |x|=|x₀|

Если данный степенной ряд расходится при x=x’₀, то он расходится  при ∀x  |x|>|x’₀|

x₀ — центр сходимости ряда.

Интервал (–R, R) называется интервалом сходимости ряда.

Число R — это радиус сходимости ряда.

Из теоремы Абеля можно сделать вывод, что существует такое значение x=R>0, при котором для |x|<R  ряд — сходится, а для |x|>R  – ряд расходится.

В соответствии с теоремой Абеля интервал [-x₀; x₀] состоит из точек сходимости. При |x₀|=R, где R – радиус сходимости, тогда интервал сходимости — (-R; R).

Для нахождения интервала сходимости степенного ряда удобно применять признаки сходимости, такие как признак Даламбера:

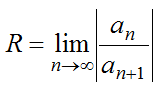
или признак Коши

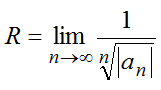
Степенной ряд внутри интервала сходимости сходится абсолютно, а вне интервала — расходится.

В случае, если  x=±R ряд может быть как расходящимся, так и сходящимся условно или абсолютно. Поэтому проблема о сходимости ряда должна решаться для каждого ряда отдельно.