Формулировка признака Коши о сходимости ряда состоит в том, что если существует предел:
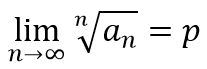
при un>0
тогда условиями сходимости и расходимости ряда по признаку Коши будут следующие:
p<1 – ряд сходится
p>1 – ряд расходится
p=1 – сходимость ряда неопределенна
Пример 1
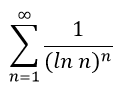
Решение
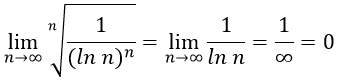
Так как 0<1, следовательно ряд сходится
Пример 2
Исследовать ряд на сходимость
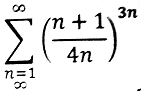
Решение
Из условия общий член ряда равен:
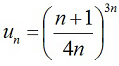
Воспользуемся радикальным признаком Коши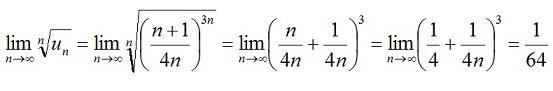
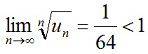
Так как меньше 1, ряд сходится.
