Понятие числового ряда

Числовой ряд – это бесконечная последовательность суммы чисел u_1, u₂,…u_n

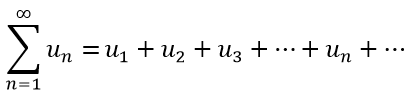
u₁ ,u₂ ,u₃ … u_n … – члены числового ряда

u_n  – общий член числового ряда.

Положительным рядом (или суммой числового ряда) называют такой ряд, у которого все члены неотрицательны, т.е.

u₁+u₂+u₃+…+u_n+…

Ряд сходится, если существует и конечен предел последовательности его частичных сумм, т.е.

S — сумма ряда.

Числовой ряд расходится, если этот предел бесконечен или не существует.

Условия эквивалентности бесконечно малых, которые применяются к рядам:

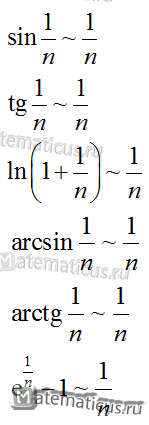
В случае применения признаков сравнения исследуемый ряд часто сравнивают с рядом геометрической прогрессии или с рядом Дирихле.

---

1. Ряд геометрической прогрессии

Пусть дан ряд геометрической прогрессии вида (здесь q — член числового ряда):

$\sum\limits_{n = 1}^\infty  {a \cdot {q^n}} $

$$a + aq + a{q^2} + … + a{q^{n — 1}} + …\quad (a \ne 0)$$

Сумма такого ряда определяется по формуле геометрической прогрессии:

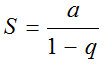
При |q|<1 — ряд сходится, а при |q|>1 — ряд расходится

---

2. Ряд Дирихле

---

Пример 1

Дан гармонический ряд

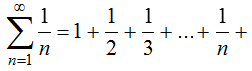
Решение

Гармонический ряд расходится, так как

---

Пример 2

Исследовать на сходимость ряд:

$$\sum\limits_{n = 0}^\infty {\frac{2}{3} \cdot \frac{1}{{{2^n}}}} = \frac{2}{3} + \frac{1}{3} + \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{24}} + …$$

Решение

Ряд представляет собой бесконечно убывающую геометрическую прогрессию

Тогда

$a = \frac{2}{3}$,  $$q = \frac{1}{2}$$

Имеем

$S = \frac{{\frac{2}{3}}}{{1 — \frac{1}{2}}} = \frac{4}{3}$