Предположим, что функция f(x) — непрерывна на промежутке [a; b) и в точке x=b имеется бесконечный разрыв и если для этой функции предел существует и конечен, то такой предел называют несобственным интегралом второго рода.
Запишем выражение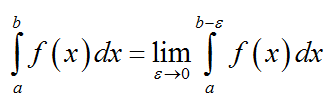
таким же образом запишем, если у функции имеется разрыв в точке x=a
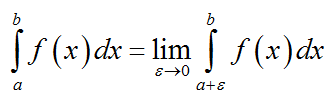
В этих случаях несобственный интеграл сходится.
Замечание
Если предел не существует или он равен бесконечности, то несобственный интеграл расходится.
Несобственный интеграл первого рода
Предположим, что функция f(x) — непрерывна на промежутке [a; +∞) и если для этой функции предел существует и конечен , то такой предел называют несобственным интегралом первого рода.
Запишем выражение
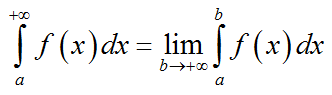
таким же образом запишем и для промежутка (-∞; b]
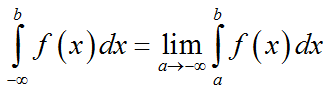
В этих случаях несобственный интеграл сходится.
Замечание
Если предел не существует или он равен бесконечности, то несобственный интеграл расходится.
