Геометрический и физический смысл производной

Геометрический смысл производной

Геометрический смысл производной заключается в том, что производная в точке x₀ равна угловому коэффициенту касательной к графику функции у = f(x) в этой точке.

f'(x₀)=tgα=k

или

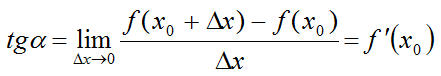
α — угол наклона касательной функции;

k — угловой коэффициент касательной.

  

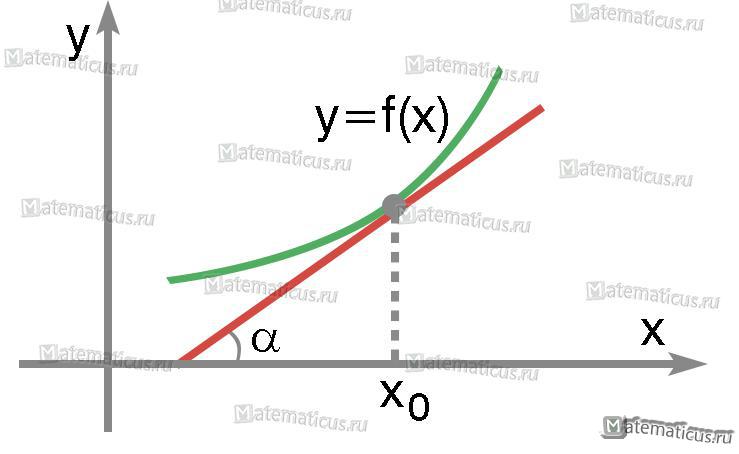
График касательной к функции при f'(x₀)=tgα>0

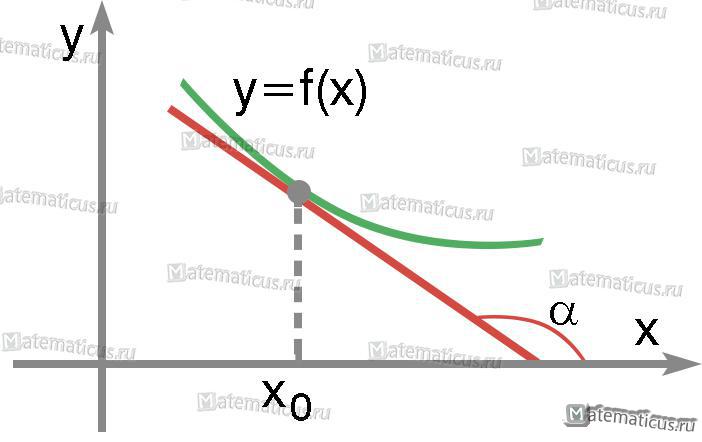
График касательной к функции при f'(x₀)=tgα<0

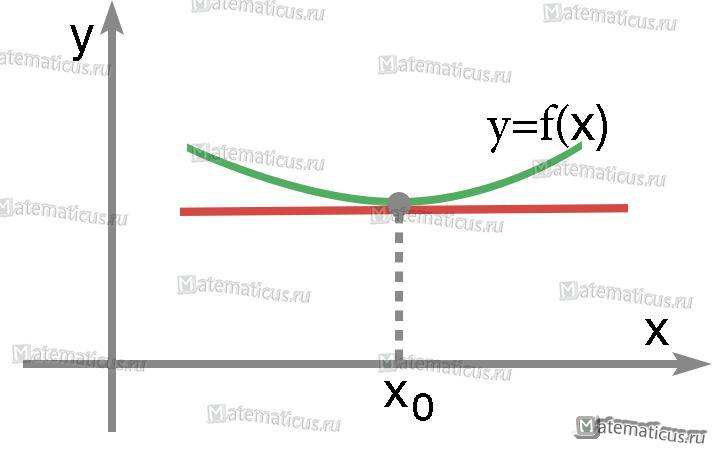
График касательной к функции при f'(x₀)=tgα=0

 Уравнение касательной к кривой:

$$y — {y_0} = f'({x_0})(x — {x_0})$$       

Уравнение нормали к кривой:

---

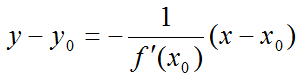
Физический смысл производной

Скорость, первая производная от перемещения по времени и находится по формуле:

V’ (t) = S(t) 

Ускорение, первая производная от скорости по времени и определяется по формуле:

a’ (t) = V (t)