Производной функцией y=f(x) в точке х=х0 называется предел отношения приращения функции в этой точке к приращению аргумента, где приращение аргумента стремится к нулю и определяется по формуле:
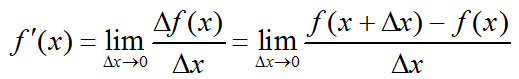
$\Delta x$ — приращение аргумента
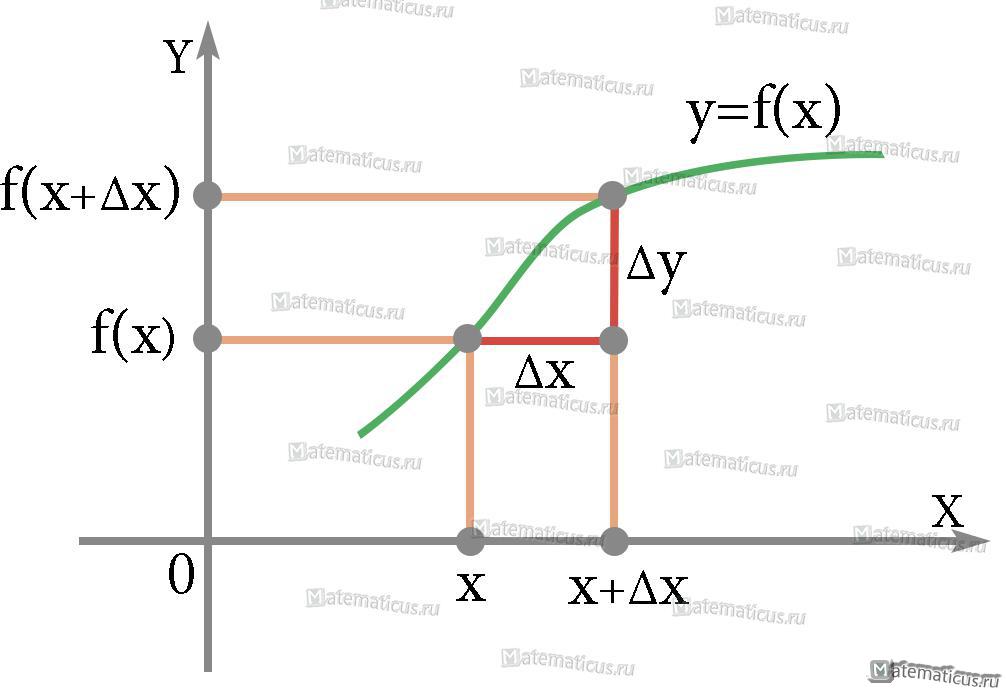
Геометрический и физический смысл рассмотрен здесь.
Пример
Найти производную функции
$$y\, = \,{x^2}$$
Решение
$$y\, = \,{x^2}$$
$$y\, + \,\Delta {\kern 1pt} y\, = \,{(x\, + \,\Delta {\kern 1pt} x)^2}$$
$$\displaylines{\,\Delta {\kern 1pt} y\, = \,{(x\, + \,\Delta {\kern 1pt} x)^2}\, — \,{x^2} = \cr= {x^2} + 2{\kern 1pt} x{\kern 1pt} \Delta {\kern 1pt} x\, + \,\Delta {\kern 1pt} {x^2} — \,{x^2} = \cr= \,2{\kern 1pt} x{\kern 1pt} \Delta {\kern 1pt} x\, + \,\Delta {\kern 1pt} {x^2} = \,\Delta {\kern 1pt} x{\kern 1pt}\,\left( {2{\kern 1pt} x\, + \,\Delta {\kern 1pt} x} \right) \cr} $$
$$\frac{{\Delta {\kern 1pt} y}}{{\Delta {\kern 1pt} x}}\,\, = \,\frac{{\Delta {\kern 1pt} x\,\left( {2{\kern 1pt} x\, + \Delta {\kern 1pt} x} \right)}}{{\Delta {\kern 1pt} x}}\, = \,2{\kern 1pt} x\, + \,\Delta {\kern 1pt} x$$
$$\mathop {\lim }\limits_{\Delta {\kern 1pt} x\, \to \,0} \frac{{\Delta {\kern 1pt} y}}{{\Delta {\kern 1pt} x}}\, = \,\mathop {\lim }\limits_{\Delta {\kern 1pt} x\, \to \,0} \left( {2{\kern 1pt} x\, + \,\Delta {\kern 1pt} x} \right)\, = \,2{\kern 1pt} x$$
Получаем
$$y’\, = {\left( {{x^2}} \right)^\prime } = \,2{\kern 1pt} x$$
