Правила дифференцирования

1. Постоянный множитель (С = const) можно вынести за знак производной:

(С·g(x))’=С·g'(x)

Пример

(2·x³)’=2·(x³)’=2·(3x²)’=6x²

---

II. Производная суммы или разности нескольких функций находится по формуле:

(f(x)±g(x)±t(x))’=f'(x)±g'(x)±t'(x)

Пример

(e^x+x^2_sin(x))’=(e^x)’+(x²)’-(sin'(x))=e^x+2x-cos(x)

---

III. Производная произведения двух функций вычисляется по формуле:

(f(x)·g(x))’=f'(x)·g(x)+f(x)·g'(x)

Пример

(e^x·x²)’=(e^x)’·x²+e^x·(x²)’=e^x·x²+e^x·2x=xe^x·(x+2)

---

IV. Производная частного от деления двух функций определяется по формуле:

 

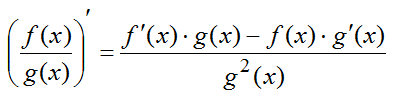
Пример

---

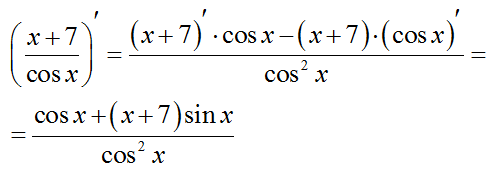
V. Производная сложной функции равна:

(f(g(x)))’=f'(g(x))·g'(x)

Пример

(sin(x⁴))’=sin'(x⁴)·(x⁴)’=cos(x⁴)·4x³=4x³·cos(x⁴)