Экстремум функции двух переменных

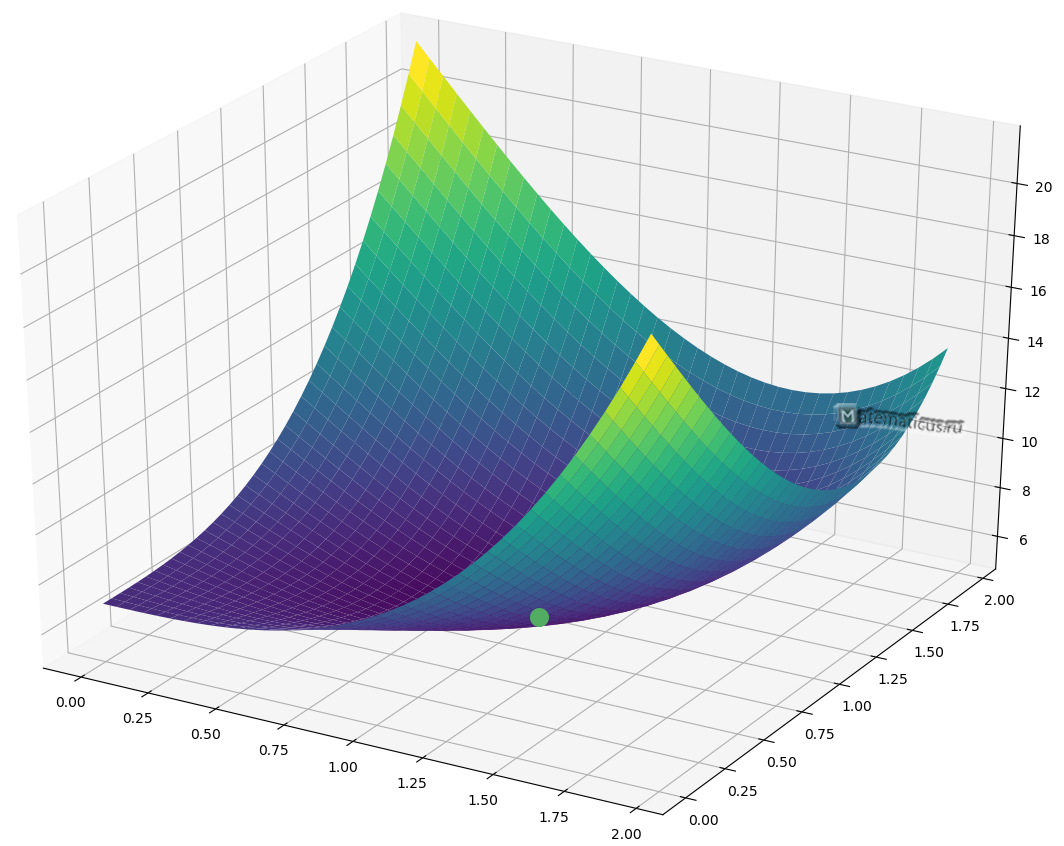
Рассмотрим достаточное условия экстремума функции двух переменных.

Выражение:

   

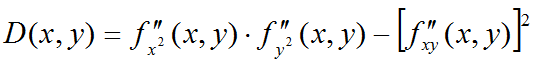
I. Если D(x₀, y₀) > 0, то в точке M(х₀, у₀) функция f(x, y) имеет экстремум,

в случае, если

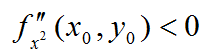
максимум,

если

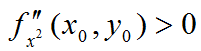минимум.

II. Если D(x₀, y₀) < 0, то в точке M(х₀, у₀) функция f(x, y) не имеет экстремума.

III. Если D = 0, то наличие экстремума под вопросом.

Необходимое условия экстремума функции двух переменных можно также определить через матрицу Гессе:

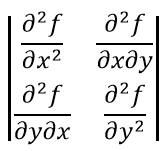
Если порядок знаков угловых миноров + и + ⇒ минимум, – и + ⇒ максимум.

---

Пример

Найти экстремум функции

z = 2x³ + 2y³ — 6xy + 7

Решение

Находим частные производные первого порядка

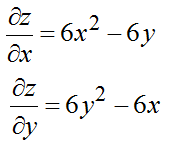
Находим критические точки, решая нелинейную систему уравнений:

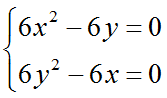
получаем две точки ${M_1}\left( {0,\,\,0} \right)$ и ${M_2}\left( {1,\,\,1} \right)$

Находим частные производные второго порядка:

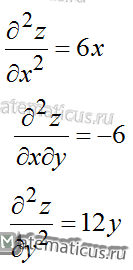
Для точки  имеем ${M_1}\left( {0,\,\,0} \right)$:

$A = 0,\,\,B =  — 6,\,\,C = 0$

и

  $\Delta  = AC — {B^2} =  — 36 < 0$

Отсюда следует, что в точке  экстремума нет.

Для точки ${M_2}\left( {1,\,\,1} \right)$ имеем:

$A = 6,\,\,B =  — 6,\,\,C = 12$

и

  $\Delta  = AC — {B^2} = 36 > 0$

$A>0, C>0$

Отсюда следует, что точке  заданная функция имеет минимум.

Найдем эту точку

z_min = 2 ·1³ + 2 ·1³ — 6 ·1 · 1 + 7 = 5

График функции двух переменных искомой функции с точкой минимума