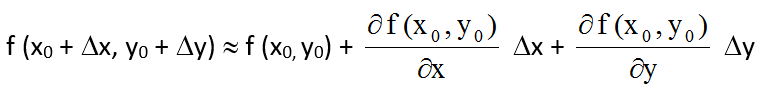Формула приближенного вычисления дифференциала:
Рассмотри пример нахождения дифференциала первого порядка в приближенных вычислениях.
Пример
Найти приближенно значение функции $f\left( {x,y} \right) = {x^3}{y^3}$ в точке M(2,03; 0,99)
Решение
Имеем
х0 = 2, y0 = 1
х= 2,03, y = 0,99
Найдем приращения аргументов:
Δx = х — х0
Δx=2,03-2=0,03
Δy = у – у0
Δy = 0,99-1=-0,01
$f\left( {{x_0},{y_0}} \right) = {2^3} \cdot {1^3} = 8$
$\frac{{\partial {\kern 1pt} {\kern 1pt} {\text{f}}\,}}{{\partial {\text{x}}}} = 3{x^2}{y^3}$
$\frac{{\partial {\kern 1pt} {\kern 1pt} {\text{f}}\,{\text{(}}{{\text{x}}_{\text{0}}}{\text{,}}{{\text{y}}_{\text{0}}}{\text{)}}}}{{\partial {\text{x}}}} = 3 \cdot {2^2} \cdot {1^3} = 12$
$\frac{{\partial {\kern 1pt} {\kern 1pt} {\text{f}}\,}}{{\partial {\text{x}}}} = 3{x^3}{y^2}$
$\frac{{\partial {\kern 1pt} {\kern 1pt} {\text{f}}\,{\text{(}}{{\text{x}}_{\text{0}}}{\text{,}}{{\text{y}}_{\text{0}}}{\text{)}}}}{{\partial {\text{x}}}} = 3 \cdot {2^3} \cdot {1^2} = 24$
f (2,03; 0,99) ≈8 + 12*0,03 + 24*( -0,01) ≈8,12
Для проверки на калькуляторе, получаем значение функции
f (2,03; 0,99)≈8,11696