Решение системы уравнений матричным способом

Матричный метод применим к решению систем линейных уравнений, в которых число уравнений равно числу неизвестных.

Пусть имеется система линейных уравнений:

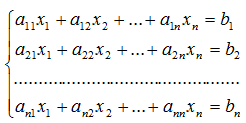
В этом уравнении введем обозначения:

где

A — матрица коэффициентов системы;

B — матрица – столбец свободных членов;

X — матрица – столбец неизвестных.

Систему уравнений запишем в матричной форме, тогда:

A×X = B

Сделаем некоторые преобразования:

A^-1×A×X = A^-1×B

т.к. А^-1×А = Е, то Е×Х = А^-1×В, получим

Х = А^-1×В — решение матричного уравнения

---

Пример

Решить систему матричным способом.

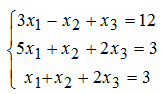
  Решение

Вычислим обратную матрицу по формуле

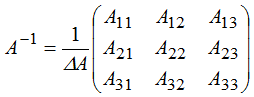
где A_ij — алгебраические дополнения к элементам матрицы.

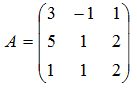
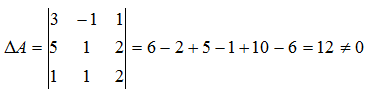
Так как определитель не равен нулю, следовательно, матрица невырожденная.

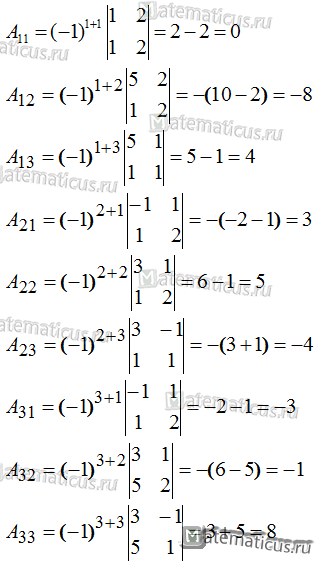
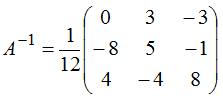
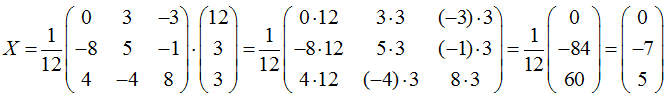
Ответ: x₁=0; x₂=-7; x₃=5