Решение системы уравнений методом Крамера

Метод применим только в том случае, если число переменных совпадает с числом уравнений в этой системе линейных уравнений.

Если определитель матрицы системы равен нулю, то искомая система имеет только одно решение

Δ = det A≠0

при

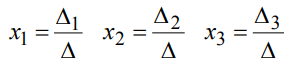
Система из n уравнений с n неизвестными

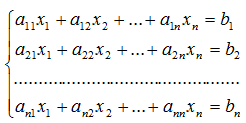
Если определитель матрицы линейной системы не равен нулю, то система имеет единственное решение.

Решение находится по формулам:

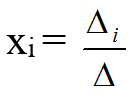
i=0,1,2…n

Δ — главный определитель, составленный из числовых коэффициентов при неизвестных,

Δ_i – вспомогательный определитель, получаемый из главного заменой i -го столбца столбцом свободных членов b_i.

---

Допустим, дана система трех линейных уравнений с тремя неизвестными, вида

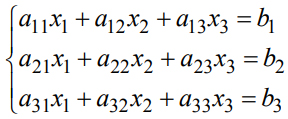
главный определитель находится по формуле:

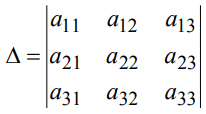
а вспомогательные по формулам:

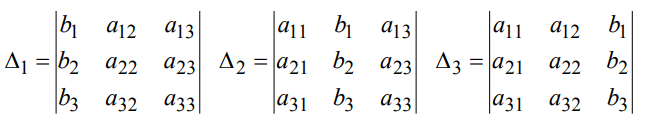
Далее по формулам Крамера находим корни искомой системы линейных уравнений:

---

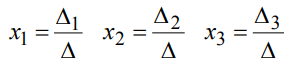
Пример 1

Решить систему линейных уравнений с двумя неизвестными с помощью метода Крамера

$\left\{ {\begin{array}{*{20}{c}}{2{x_1}}& + &{3{x_2}}& = &{ — 1} \\ {3{x_1}}& + &{4{x_2}}& = &{ — 1} \end{array}} \right.$

Решение

$\left\{ {\begin{array}{*{20}{c}}{2{x_1}}& + &{3{x_2}}& = &{ — 1} \\ {3{x_1}}& + &{4{x_2}}& = &{ — 1} \end{array}} \right.$

Находим определитель матрицы второго порядка системы

$\Delta  = \left| {\begin{array}{*{20}{c}}2&3 \\ 3&4 \end{array}} \right| = 8 — 9 =  — 1 \ne 0$

Имеем:

${\Delta _{\,1}} = \left| {\begin{array}{*{20}{c}} { — 1}&3 \\ { — 1}&4 \end{array}} \right|=$

$=  — 1 \cdot 4 — 3 \cdot ( — 1) =  — 1$

${\Delta _2} = \left| {\begin{array}{*{20}{c}}  2&{ — 1} \\  3&{ — 1} \end{array}} \right|=$

$= 2 \cdot ( — 1) — 3 \cdot ( — 1) = 1$

Следовательно, находим корни уравнения

${x_{\,1}} = \frac{{{\Delta _{\,1}}}}{\Delta } = \frac{{ — 1}}{{ — 1}} = 1$

${x_2} = \frac{{{\Delta _2}}}{\Delta } = \frac{1}{{ — 1}} =  — 1$

---

Пример 2

Решить систему линейных уравнений  с тремя неизвестными с помощью метода Крамера

$\left\{ {\begin{array}{*{20}{c}}{3{x_1} — {x_2} + {x_3} = 12} \\  {5{x_1} +{x_2} + 2{x_3} = 3} \\ {x{}_1 + {x_2} + 2{x_3} = 3} \end{array}{\text{ }}} \right.$

Решение

Найдем определитель матрицы третьего порядка, по формуле:

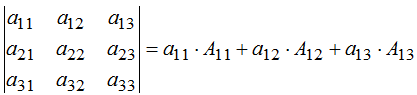
Определитель матрицы равен:

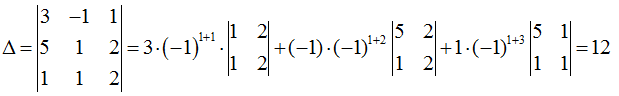
Определитель не равен нулю

Вычислим вспомогательные определители

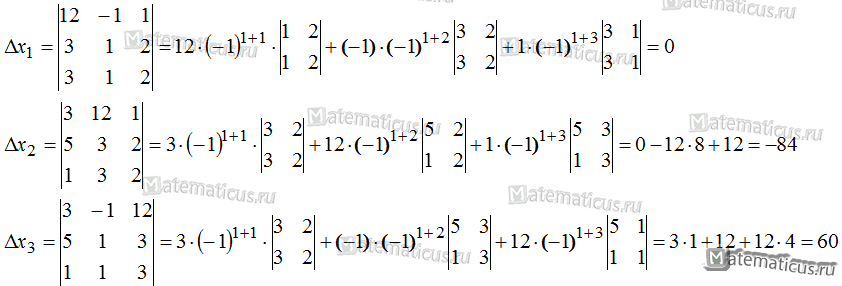
Тогда получаем окончательное решение

${x_1} = \frac{{\Delta {x_1}}}{\Delta } = \frac{0}{{12}} = 0$

${x_2} = \frac{{\Delta {x_2}}}{\Delta } =  — \frac{{84}}{{12}} =  — 7$

${x_3} = \frac{{\Delta {x_3}}}{\Delta } = \frac{{60}}{{12}} = 5$

Ответ: x₁=0; x₂=-7; x₃=5