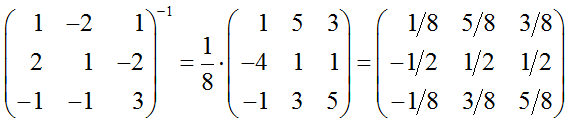Пусть дана матрица:
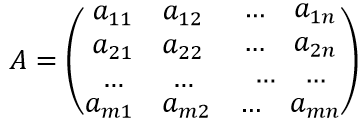
где определитель этой матрицы не равен нулю, т.е.
det(A) ≠ 0
то существует единственная матрица
А∙А-1 = А-1∙А = Е
где А-1 — обратная матрица и находится по формуле:
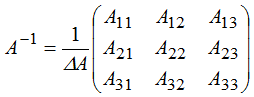
где
ΔA — определитель матрицы A;
Aij — алгебраические дополнения к элементам aij матрицы A и находится по формуле:
Аij = (-1)i+j ∙Mij
Mij — минор
Более подробно нахождения обратной матрицы рассмотрим на примере.
Пример
Дана квадратная матрица.
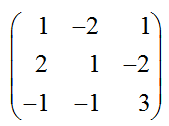
Требуется найти обратную матрицу.
Решение
Формула обратной матрицы выражается зависимостью:
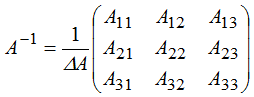
Находим определитель матрицы третьего порядка:
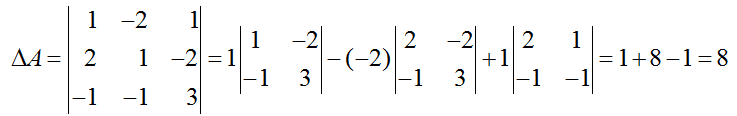
Находим миноры:
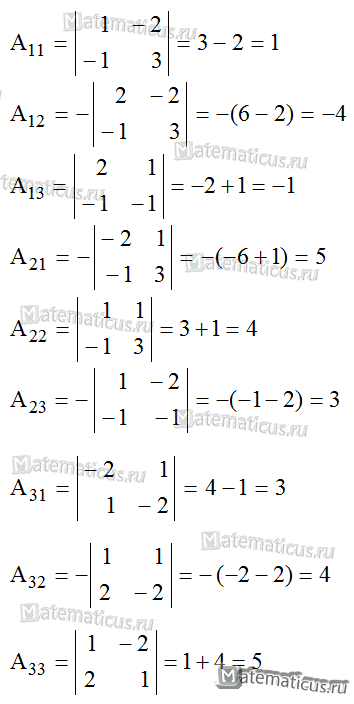
Подставляя полученные значения в формулу, получаем обратную матрицу