Равенство вида:
$${e^{x + iy}} = {e^x}(\cos y + i\sin y)$$
называется уравнением Эйлера
Это уравнение определяется из равенства
$${e^z} = \mathop {\lim }\limits_{n \to \infty } {\left( {1 + \frac{z}{n}} \right)^n}$$
Если примем , то получим соотношение:
$${e^{iy}} = \cos y + i\sin y$$
$$\eqalign{& {e^{i\pi /4}} = \cos \left( {\frac{\pi }{4}} \right) + i\sin \left( {\frac{\pi }{4}} \right) = \cr & = \frac{{\sqrt 2 }}{2} + i\left( {\frac{{\sqrt 2 }}{2}} \right) \cr} $$
В частности запишем равенство для комплексно–сопряженного числа:
$${e^{ — iy}} = \cos y — i\sin y$$
Из этих уравнений получаем:
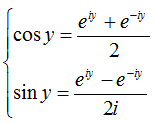
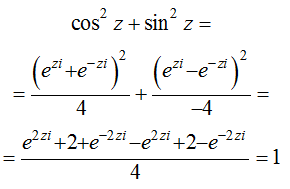
Если комплексное число записать в тригонометрической форме:
$$z = r(\cos \phi + i\sin \phi )$$
и подставить в него уравнение Эйлера:
$${e^{i\phi }} = \cos \phi + i\sin \phi $$
то получим показательную форму комплексного числа
$$z = |r|{e^{i\phi }}$$
