Функция f(x) называется непрерывной в точке x₀, если:

I. функция определена в этой точки;
II. существует предел

$$\mathop {\lim }\limits_{x \to {x_0}} f(x)$$

III. этот предел равен значению функции в точке x₀, т.е.

$$\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})$$

На рисунке ниже представлена непрерывная функция y=cosx.

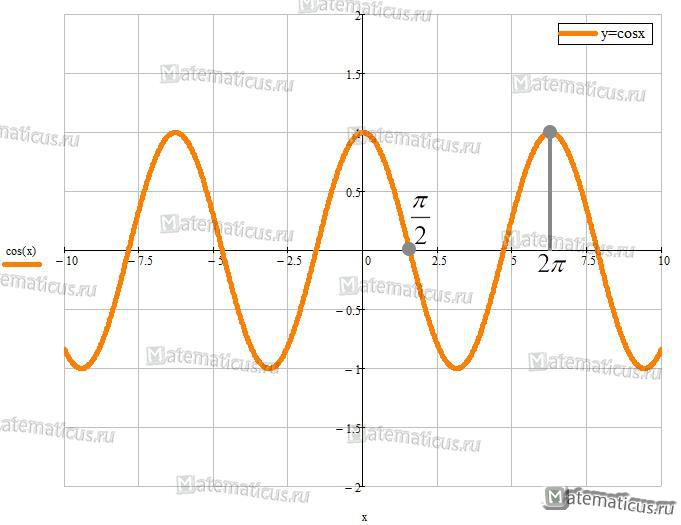
График функции y=cosx

Точками разрыва функции называют точки, в которых нарушается непрерывность функции.

Разрыв первого рода

Если пределы $\mathop {\lim }\limits_{x \to {x_0} — 0} f(x)$ и $\mathop {\lim }\limits_{x \to {x_0} + 0} f(x)$ существуют и конечны, но не равны друг другу

Разрыв второго рода

Если один из односторонних пределов (правый или левый) функции в точке равен бесконечности или не существует.

---

Пример 1
Показать, что при x=2 функция $y = \frac{x}{{x — 2}}$ имеет разрыв
Решение
$$\mathop {\lim }\limits_{x \to 2 — 0} \frac{x}{{x — 2}} =  — \infty $$
$$\mathop {\lim }\limits_{x \to 2 + 0} \frac{x}{{x — 2}} =  + \infty $$
Функция $y = \frac{x}{{x — 2}}$ при x→2 не имеет ни левого и ни правого конечного предела ⇒  точка имеет разрыва второго рода.

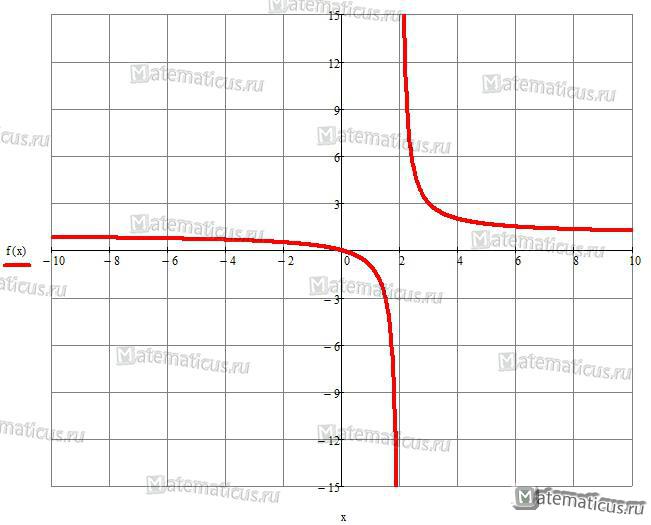
График функции $y = \frac{x}{{x — 2}}$

---

Пример 2
Показать, что при x=0 функция $y = arctg\frac{1}{x}$ имеет разрыв
Решение
$$\mathop {\lim }\limits_{x \to  — 0} arctg\frac{1}{x} =  — \frac{\pi }{2}$$
$$\mathop {\lim }\limits_{x \to  + 0} arctg\frac{1}{x} = \frac{\pi }{2}$$
Функция $y = arctg\frac{1}{x}$ при x→0 имеет конечные различные левый и правый пределы ⇒  точка имеет разрыва первого рода.

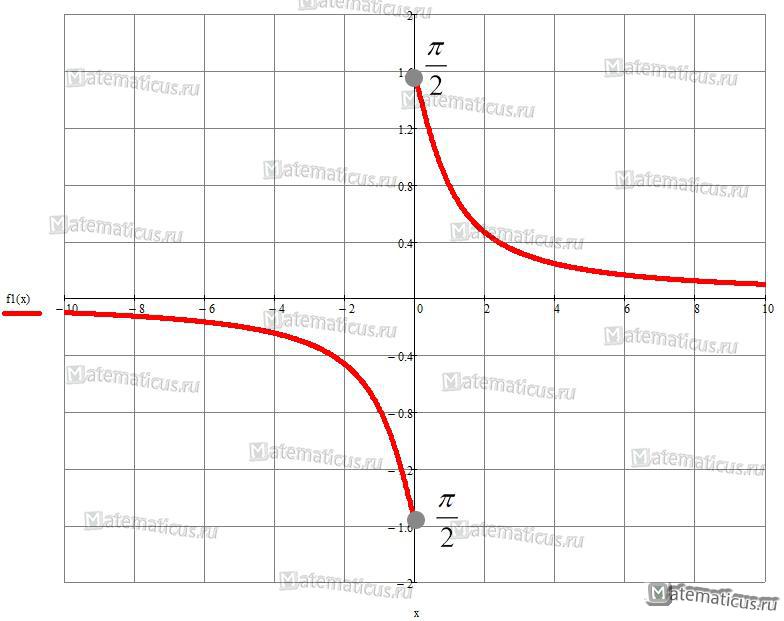 График функции $y = arctg\frac{1}{x}$