Достаточное и необходимое условие существования экстремума функции
Экстремум функции — это максимум и минимум непрерывной функции y=f(x) непрерывна в критической точке x0.
Условие максимума функции
Если производная от функции больше нуля при
f′(x)>0 при x<x0, x0 — точка максимума
Если производная от функции меньше нуля при
f′(x)<0 при x>x0, x0 — точка максимума
Условие минимума функции
Если производная от функции меньше нуля при
f′(x)<0 при x<x0, x0 — точка максимума
Если производная от функции больше нуля при
f′(x)>0 при x>x0, x0 — точка максимума
Условие экстремума функции через нахождения второй производной
При f′′(x0)≠0 и f′′(x0)<0 — максимум
При f′′(x0)≠0 и f′′(x0)>0 — минимум
С помощью второй производной определяется вогнутость и выпуклость функции
Пример
Найти экстремумы функции
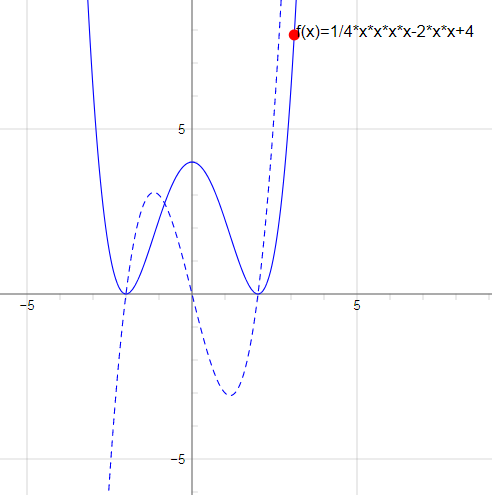
$y=\frac{x^{4}}{4}-2x^{2}+4$
Решение
Найдём производную от функции
y′=x3–4x
Определите количество точек экстремума функции
Найдём критические точки функции
x(x2–4)=0
x(x–2)(x+2)=0
Отсюда
x1=–2; x2=0; x3=2
Точки экстремума функции на отрезке
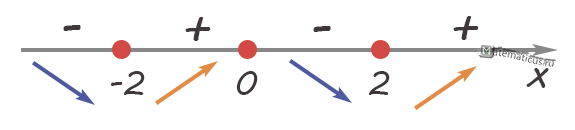
Точками экстремума функции являются:
f(–2)=0 — минимум;
f(0)=4 — максимум;
f(2)=0 — минимум.
Получается три точки экстремума функции.
Построим график функции онлайн здесь
Пунктирной линией на графике показана производная функция