Формула для вычисления длины дуги кривой заданной уравнением у=f(x) в прямоугольной системе координат:
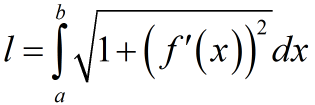
a — начала дуги по оси OX;
b — конец дуги по оси OX a<b.
Если плоская кривая задана уравнением x=g(y) то формула имеет вид:
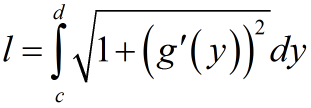
c — начала дуги по оси OY;
d — конец дуги по оси OY a<b
Если кривая задана в полярных координатах r=r(φ), α≤φ≤β, то длина дуги вычисляется по формуле:
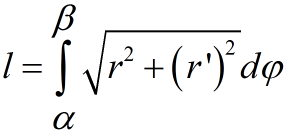
Если кривая задана параметрическим уравнением вида x=x(t) и y=y(t), то длина дуги определяется по формуле
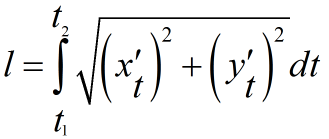
t2, t1 — значения параметров, которые соответствуют концам дуги t1<t2
Пример 1
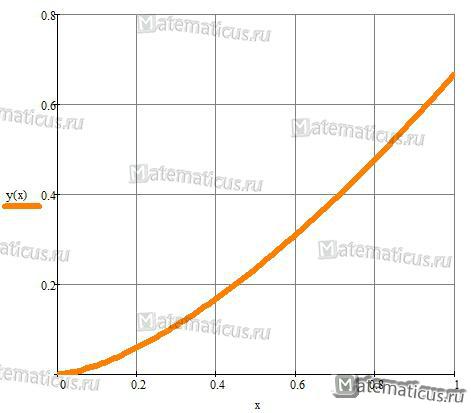
Найти длину дуги функции на промежутке от 0 до 1.
$$y = \frac{2}{3}{x^{\frac{3}{2}}}$$
Решение
Найдем производную функции:
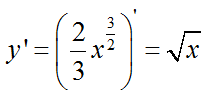
Возведём в квадрат функцию:
$$(\sqrt x ) = x$$
Подставляя в формулу, найдем длину дуги:
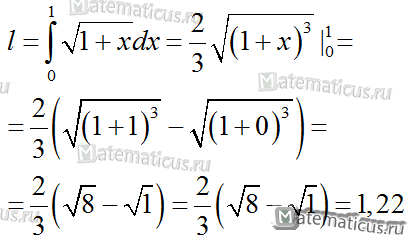
Пример 2
Найти длину дуги окружности от точки ${M_1}\left( {4;0} \right)$ до точки ${M_2}\left( {2\sqrt 2 ;2\sqrt 2 } \right)$. Уравнение окружности задано в параметрическом виде.
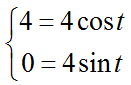
Решение
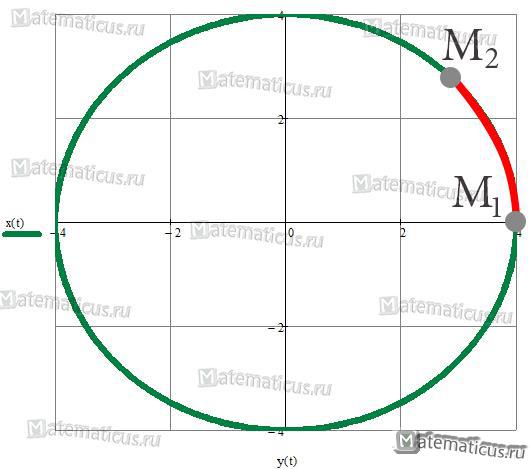
Найдем параметр t в точках M1 и M2, решим системы уравнений.
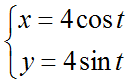
Здесь t1=0
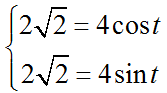
Отсюда ${t_2} = \frac{\pi }{4}$
Подставляя в формулу, найдем длину дуги окружности.
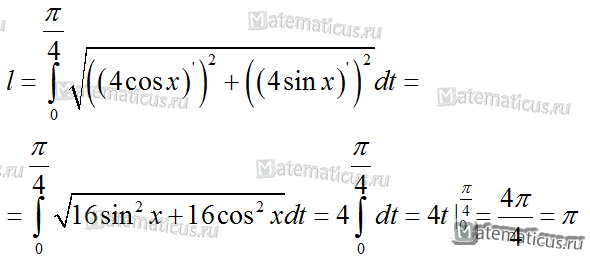
Пример 3
Вычислить длину дуги одного лепестка циклоиды. Уравнение циклоиды задано параметрическим уравнением.
$$x = t — \sin t$$
$$y = 1 — \cos t$$
Решение
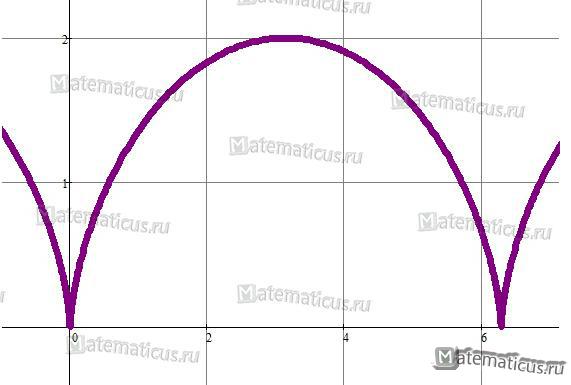
График циклоиды
Продифференцируем по t параметрические уравнения циклоиды:
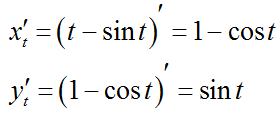
отсюда
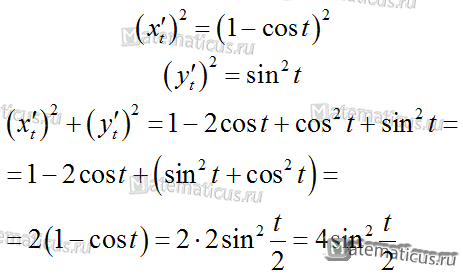
Подставляя в формулу, получаем
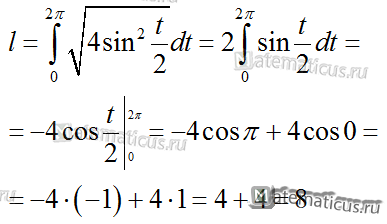

Была бы оценка 5, если бы не дурак, который не от большого ума изукрасил весь текст, особенно формулы и ответы, серыми узорами! Сколько времени и усилий ушло на расшифровку ответов! Так что 3,5 балла — это ещё слишком много! Так и передайте идеологу этой мазни!
Каждому своё, информация важная, а что написано между строк, неважно. Очень интересная статья, спасибо!